
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 10. Матрицыи -единичные матрицы
|
|
|
|
Пример 9. Матрицыи -диагональные матрицы.
Пример 8.Матрицыи -диагональные матрицы.
Определение 11. Диагональная матрица 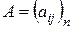 называется скалярной, если все элементы главной диагонали принимают одинаковые значения.
называется скалярной, если все элементы главной диагонали принимают одинаковые значения.
Определение 12. Скалярная матрица 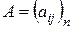 называется единичной, если все элементы главной диагонали матрицы равны 1, т.е.
называется единичной, если все элементы главной диагонали матрицы равны 1, т.е. 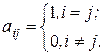
Обозначение: E или  , когда требуется указать размер матрицы, т.е.
, когда требуется указать размер матрицы, т.е.
 , где
, где 
Теорема 2. Если  , где
, где  то для любой матрицы
то для любой матрицы 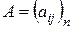
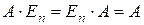 . (14)
. (14)
Доказательство.
Пусть матрица  , тогда, согласно определению 7, матрица
, тогда, согласно определению 7, матрица  , где
, где
 , так как
, так как 
Пусть матрица  , тогда, согласно определению 7, матрица
, тогда, согласно определению 7, матрица 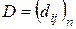 , где
, где
 , так как
, так как 
Из полученных результатов следует, что 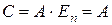 и
и  , следовательно,
, следовательно, 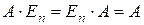 . Утверждение доказано.
. Утверждение доказано.
Следствие 1. Если матрица 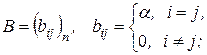 где
где 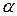 - некоторое число, т.е. B - cкалярная матрица порядка n, то для любой матрицы
- некоторое число, т.е. B - cкалярная матрица порядка n, то для любой матрицы 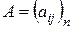
 . (15)
. (15)
Доказательство. Нетрудно заметить, что  . Следовательно,
. Следовательно,
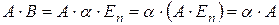 ;
;  .
.
Что и требовалось доказать.
Определение 13. Операция перехода от матрицы  к матрице
к матрице  , где
, где  ,
, 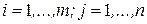 , т.е. когда столбцы матрицы А превращаются в соответствующие строки матрицы В, называется транспонированием матрицы А. Матрица В в этом случае называется транспонированной матрицей А.
, т.е. когда столбцы матрицы А превращаются в соответствующие строки матрицы В, называется транспонированием матрицы А. Матрица В в этом случае называется транспонированной матрицей А.
Обозначение: 
Пример 11.  ,
,  .
.
Замечание. Нетрудно заметить, что при транспонировании матриц элементы, стоящие на главной диагонали, не изменяю своего положения.
Теорема 3 (свойства операции транспонирования)
1)  , где
, где  - единичная матрица порядка n.
- единичная матрица порядка n.
2)  , для любых матриц
, для любых матриц  .
.
3)  , где
, где  и
и  (16)
(16)
4)  , где
, где 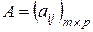 и
и  . (17)
. (17)
5) 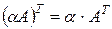 , для любых матриц А и любых постоянных
, для любых матриц А и любых постоянных 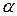 .
.
Доказательство. Справедливость свойств 1 и 2 следует из определения 13. Следовательно, доказать требуется лишь свойства 3 и 4.
3) Пусть  .
.
Так как  ,
,  , то для матрицы
, то для матрицы  , где
, где 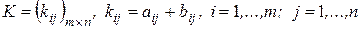 .
.
Следовательно,  , и, согласно определению 13,
, и, согласно определению 13,  , где
, где
 ,
, 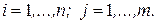 (18)
(18)
Пусть  . Так как
. Так как  ,
,  , то матрица
, то матрица  - матрица вида
- матрица вида  , где
, где 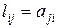 ,
,  а матрица
а матрица  - матрица вида
- матрица вида  , где
, где  ,
, 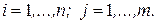
Следовательно, 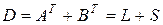 и
и  , где
, где
 ,
, 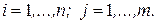 (19)
(19)
Из формул (18) и (19) следует, что  ,
, 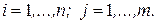 Это означает равенство матриц С и D, а значит, и справедливость формулы (16). Утверждение 3 доказано.
Это означает равенство матриц С и D, а значит, и справедливость формулы (16). Утверждение 3 доказано.
4) Применяем ту же методику: доказываем, что матрицы в левой и правой части равенства (17) состоят из одинаковых элементов.
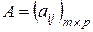 ,
,  , тогда
, тогда 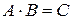 , где
, где  , элементы которой определяются по формуле (20):
, элементы которой определяются по формуле (20):
 ,
, 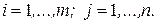 (20)
(20)
Пусть 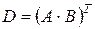 , тогда
, тогда 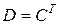 и, согласно определению 13,
и, согласно определению 13,  , где
, где  ,
, 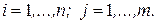 В этом случае, из (20) следует, что элементы матрицы определяются по формулам (21):
В этом случае, из (20) следует, что элементы матрицы определяются по формулам (21):
 ,
, 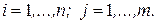 (21)
(21)
Так как 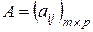 ,
,  , то матрица
, то матрица  - матрица вида
- матрица вида  , где
, где 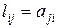 ,
, 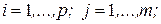 а матрица
а матрица  - матрица вида
- матрица вида 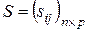 , где
, где  ,
, 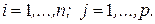
Следовательно, матрица 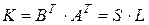 ,
,  , элементы которой определяются по правилу:
, элементы которой определяются по правилу:
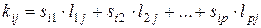 ,
, 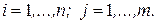 (22)
(22)
Используя представления элементов матриц L и S с помощью элементов матриц А и В, получаем:
 ,
, 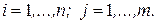 (23)
(23)
Из равенств (21) и (23) следует, что элементы матриц D и К, стоящие на одинаковых местах, совпадают, значит,  , что означает, что
, что означает, что  . Утверждение доказано.
. Утверждение доказано.
5) Данное свойство докажите самостоятельно.
Определение 14. Элементарными преобразованиями матриц называются следующие операции над матрицами:
1) перестановка двух строк матрицы местами;
2) умножение всех элементов некоторой строки матрицы на одно и то же число;
3) прибавление к элементам некоторой строки матрицы соответствующих элементов другой строки этой же матрицы, умноженных на число;
4) те же операции над столбцами.
Определение 15. Матрицы А и В, получающиеся одна из другой при помощи элементарных преобразований, называются эквивалентными.
Обозначение:  .
.
Смысл этой эквивалентности станет Вам понятен позднее, в частности, при исследовании систем линейных уравнений.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 420; Нарушение авторских прав?; Мы поможем в написании вашей работы!