Пример 12

а) 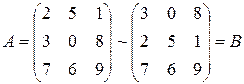. Здесь у матрицы A поменяли первую и вторую строку местами.

б) 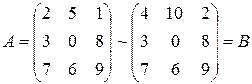. Здесь у матрицы A все элементы первой строки умножили на число 2.

в) . Здесь к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на 2.

Определение 16. Матрица называется матрицей треугольного вида, если все элементы, расположенные ниже элементов 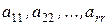, , 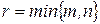в соответствующих столбцах, т.е. ниже главной диагонали, равны нулю.

Пример 13. Матрицы 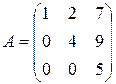, , 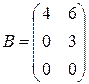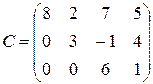- матрицы треугольного вида.

Замечание. Иногда треугольные матрицы рассмотренного вида называют правыми верхними треугольными матрицами. Соответственно, матрицы, у которых все элементы, расположенные выше элементов 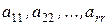, , 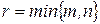в соответствующих столбцах (т.е. выше главной диагонали), равны нулю, называют левыми нижними треугольными матрицами (Шев. КР., стр. 118). Используя побочную диагональ 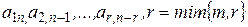, можно, соответственно, также ввести левую верхнюю и правую нижнюю треугольные матрицы.

Так как для изложения рассматриваемого нами курса достаточно использования треугольных матриц правого верхнего вида, далее во всех случаях мы их будем называть просто матрицами треугольного вида.

Теорема 3. Любая матрица с помощью элементарных преобразований может быть приведена к треугольному виду.

Доказательство. Проведите самостоятельно.

Справедливость данного утверждения легко подтвердить на следующем примере.

Дата добавления: 2015-08-31