Спектральное преобразование сигнала

Поскольку любой звук раскладывается на синусоидальные волны, мы можем построить частотный спектр звука. Спектр частот звуковой волны представляет собой график зависимости амплитуды от частоты.

Фазовые изменения часто происходят по причине временных задержек. Например, каждый цикл сигнала в 1000 Гц занимает 1/1000 секунды. Если задержать сигнал на 1/2000 секунды (полупериод), то получится 180-градусный сдвиг но фазе. Заметим, что этот эффект опирается на зависимость между частотой и временной задержкой. Если сигнал в 250 Гц задержать на те же самые 1/2000 секунды, то будет реализован 45-градусный сдвиг по фазе.

Если сложить вместе две синусоидальные волны одинаковой частоты, то получится новая синусоидальная волна той же частоты. Это будет верно даже в том случае, если два исходных сигнала имеют разные амплитуды и фазы. Например, Asin(2 Pi ft) и Bcos(2 Pi ft) две синусоиды с разными амплитудами и фазами, но I c одинаковой частотой.

Для измерения амплитуды одной частоты нужно умножить имеющийся сигнал на синусоиду той же частоты и сложить полученные отсчеты.
Чтобы записать это в символьном виде, предположим, что отсчеты имеют значения s0, s1, …, st, …. Переменная t представляет собой номер отсчета (который заменяет значение времени). Измеряется амплитуду частоты f в первом приближении, при вычислении следующей суммы:

Значения t и f не соответствуют в точности времени и частоте. Более того, f – целое число, а реальная исследуемая частота – это частота дискретизации, умноженная на f/N. Подобным образом, t — это целочисленный номер отсчета. Кроме того, суммирование дает не непосредственное значение амплитуды, а всего лишь число, пропорциональное амплитуде.

Если повторить эти вычисления для различных значений f, то можно измерить амплитуду всех частот в сигнале. Для любого целого f меньшего N легко определяется значение Аf, представляющее амплитуду соответствующей частоты как долю от общего сигнала. Эти значения могут быть вычислены по той же формуле:

Если мы знаем значения Af мы можем восстановить отсчеты. Для восстановления сигнала необходимо сложить все значения для разных частот. Чтобы осуществлять точное обратное преобразование Фурье, помимо амплитуды и частоты необходимо измерять фазу каждой частоты.

Для этого нужны комплексные числа. Можно изменить описанный ранее метод вычислений так, что он будет давать двумерный результат. Простое коми1 лексное число – это двумерное значение, поэтому оно одновременно но представляет и амплитуду, и фазу.
При таком подходе фазовая часть вычисляется неявно. Вместо амплитуды и фазы измеряется две амплитуды, соответствующие разным фазам. Одна из этих фаз представляется косинусом (соs()), другая синусом sin()).
Используя комплексные числа, можно проводить измерения одновременно, умножая синусную часть на -i.

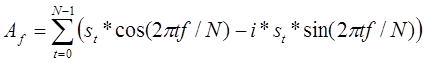
Каждое значение Af теперь представляется комплексным числом; действительная и мнимая части задают амплитуду двух синусоидальных волн с разным фазами.

Основная идея быстрого преобразования Фурье заключается в том, что каждую вторую выборку можно использовать для получения половинного спектра. Формально это означает, что формула дискретного преобразования Фурье может быть представлена в виде двух сумм. Первая содержит все четные компоненты оригинала, вторая — все нечетные

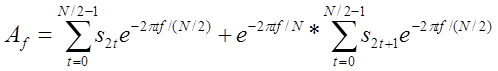
Фильтрация спектра.
Получив спектральное представление сигнала его требуется отчистить от шумов. Человеческий голос обладает известными характеристиками, и поэтому те области которые не могут являются характеристиками голоса нужно погасить. Для этого применим функцию, которая получила название «окно Кайзера»


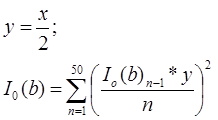
После фильтрации спектра наложим окно Ханнинга

Сравнение с эталонными образцами в базе
Основным параметром, используемым для идентификации, является мера сходства двух звуковых фрагментов. Для ее вычисления необходимо сравнить спектрограммы этих фрагментов. При этом сначала сравниваются спектры, полученные в отдельном окне, а затем вычисленные значения усредняются.

Для сравнения двух фрагментов использовался следующий подход:
Предположим что X[1..N] и Y[1..N] массивы чисел, одинакового размера N, содержащие значения спектральной мощности первого и второго фрагментов соответственно. Тогда мера сходства между ними вычисляется по следующей формуле:

где Mx и My математические ожидания для массивов X[] и Y[] соответственно, вычисляющиеся по следующей формуле:

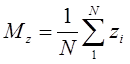
Данный способ вычисления меры сходства двух фрагментов представленных в виде спектра является самым оптимальным для задачи идентификации человека по его голосу.

Дата добавления: 2015-08-31