
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Режим гололеда с ветром 3 страница
|
|
|
|
Это допущения будет принято,при этом подрессорный токопремник и контактную подвеску можно считать за колебательную систему с двумя степенями свободы,схема замещения которой представлена на рисунке 3.8
Первое тело образуют подъемные рамы токоприемника с приведенной массой 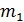 ,второе
,второе  полоз токоприемника
полоз токоприемника  ,находящийся в контакте с подвеской,приведенная масса которой равна
,находящийся в контакте с подвеской,приведенная масса которой равна  , при этом
, при этом  =
=  .Под
.Под  обозначена обобщенный коэффициент жесткости нижнего узла токоприемника включающего подъемную и опускающую пружины и элементы их крепления,под
обозначена обобщенный коэффициент жесткости нижнего узла токоприемника включающего подъемную и опускающую пружины и элементы их крепления,под 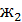 обобщенный коэффициент жесткости
обобщенный коэффициент жесткости  верхний узел токоприемника
верхний узел токоприемника  контактная подвеска
контактная подвеска

Рисунок 3.8 К расчету главных колебаний токопремник  контактная подвеска
контактная подвеска
Определим частоты и формы главных колебаний этой системы,используя метод обобщенных координат Лагранжа.За основу расчета принят токоприемник 17РР,снабженный устройством подрессоривания полоза и подвески КС  200 для высокоскоростного движения.Характеристика элементов контактной сети представлена в таблице 3.2
200 для высокоскоростного движения.Характеристика элементов контактной сети представлена в таблице 3.2
Таблица 3.2 - К расчету динамических характеристик токоприемника 17РР
| Элементы | Масса m,кг | Длинна
 ,м ,м
| Жесткость Ж,H/м |
| Трубы нижних рам | 6,43 | 1,2 | 
|
| Трубы верхних рам | 6,29 | 1,58 | 
|
| Полоз | 15,9 | 2,260 | 
|
| Главный вал | 21,6 | 1,24 | 
|
| Раскос | 6,76 | 2,01 | 
|
| Держатель | 4,85 | 1,100 | 
|
| Рычаг | 5,7 | 0,24 | 
|
| Пружина подъемная | 
| 
| 8,75* 
|
| Развернутая длина в,мм | |||
| Пружина1каретки* | 
| 2,94* 
| |
| Пружина2каретки* | 
| 6* 
|
Приведенную массу рам токоприемника (без полоза) определяем,исходя из схемы конструкции представленной на рисунке 3.9
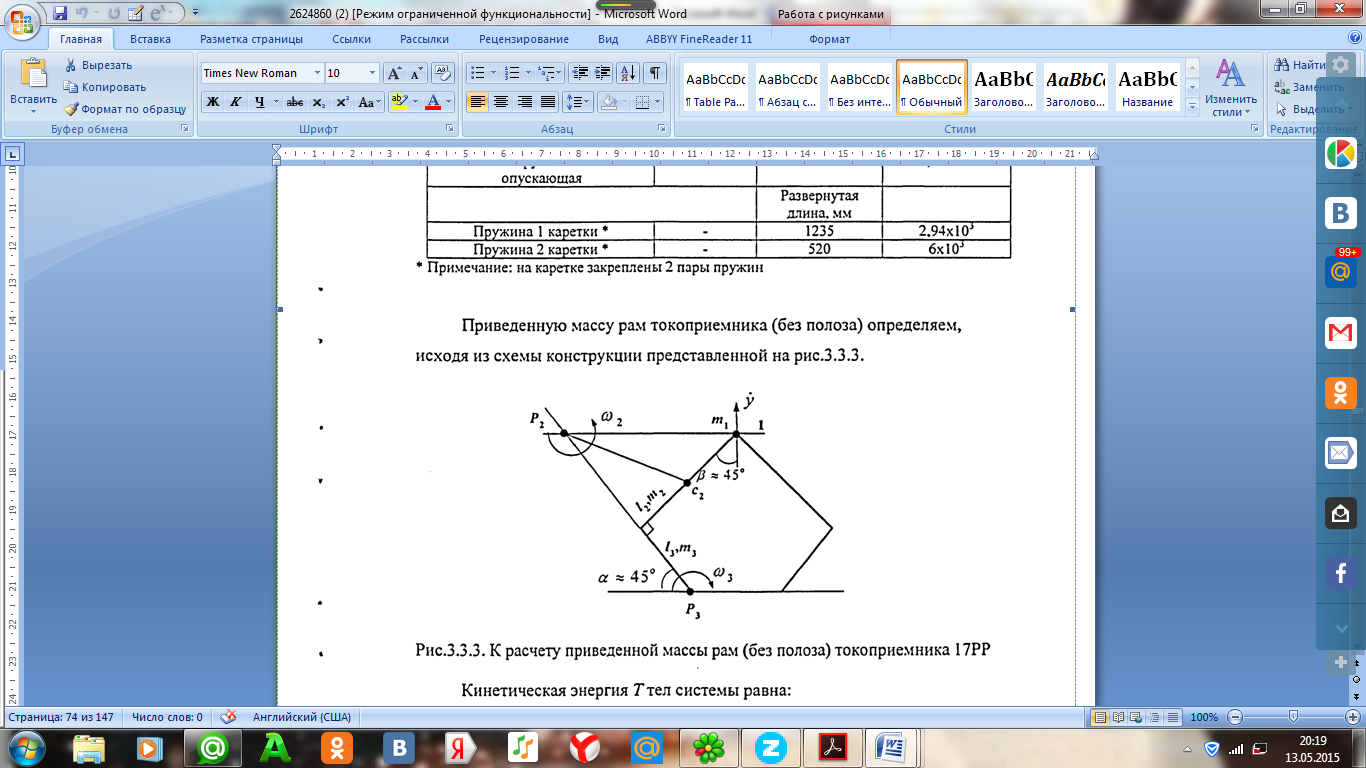
Рисунок 3.9 К расчету приведенной массы рам(без полоза) 17РР
Кинетическая энергия Т тел системы равна:
Т= 
где  =
=  – кинетическая энергия верхнего шарнира токоприемника;
– кинетическая энергия верхнего шарнира токоприемника;
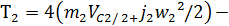 кинетическая энергия труб верхней рамы токоприемника;
кинетическая энергия труб верхней рамы токоприемника;  =4(
=4( /2) – кинетическая энергия нижней рамы токоприемника.Здесь
/2) – кинетическая энергия нижней рамы токоприемника.Здесь  - скорость поступательного движения центра тяжести каждой из труб верхней рамы;
- скорость поступательного движения центра тяжести каждой из труб верхней рамы;  и
и  угловые скорости вращения труб верхней и нижней рам относительно осей показанных на рисунке
угловые скорости вращения труб верхней и нижней рам относительно осей показанных на рисунке  и
и 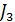 –момент инерции труб относительно этих осей вращения.
–момент инерции труб относительно этих осей вращения. 
Расчеты для состояния токоприемника,при котором трубы верхних и нижних рам образуют между собой прямой угол показывают,что кинетическая энергия движущихся в вертикальном направлении рам токоприемника Т равна;
Т=  .
.
Отсюда приведенная к верхнему шарнирному узлу масса рам токоприемника(без полоза) равна;
 (3.42)
(3.42)
Масса полоза  =15,9кг у опоры и
=15,9кг у опоры и  ,приведенная масса подвески
,приведенная масса подвески  как видно из таблицы 1.2.3
как видно из таблицы 1.2.3  =40…55кг у опоры
=40…55кг у опоры  =30…45кг в середине пролета.Поэтому значения массы
=30…45кг в середине пролета.Поэтому значения массы  ,будут для этих случаев равны
,будут для этих случаев равны  =55,9…70,9кг и
=55,9…70,9кг и  =45,9…60,9кг соответственно.
=45,9…60,9кг соответственно.
Основные характеристики контактных подвесок для высоких скоростей движения представлены в таблице 3.3
Таблица 3.3 – Характеистика контактных подвесок для высоких скоростей э.п.с
| Контактная подвеска | V,км/ч | L,м | Значение 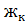 ,Н/м ,Н/м
| Значение 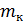 ,кг ,кг
| ||
| у опоры | в середине пролета | у опоры | в середине пролета | |||
| С одним контактным проводом | 

| 

| ||||
| С двумя Контакным проводом | 

| 

| ||||
| С одним Контактным проводом | 55 70 55 70 |

|

| 25…40 25…35 25…55 30…45 | 20…30 25…30 25…45 25…35 | |
| С двумя Контактным проводом |

|

| 30…55 30…45 30…60 40…55 | 25…40 30…40 30…55 30…45 |
Обобщенный коэффициент жесткости подъемной и опускающей пружин нижних рам токоприемника для его формы показанной на рисунке определялось по формуле:
 = ж*b
= ж*b  (3.43)
(3.43)
где b,ж- длина рычага подъемной (опускающей) пружины и ее жесткость соответственно,м; 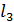 - длины трубы нижней рамы,м.
- длины трубы нижней рамы,м.
Подставляя из таблицы 3.2 характеристики 17РР значения ж,b и 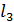 численное значение
численное значение  вертикальной
вертикальной  жесткости нижней части токоприемника (без пружин подрессоривающих полоз)
жесткости нижней части токоприемника (без пружин подрессоривающих полоз)  =1,24*
=1,24*  Н/м.
Н/м. 
Все пружины,относящиеся к верхнему узлу токоприемника,а также  пружина
пружина  являющаяся эквивалентом жесткости контактной подвески соеденены параллельно,как это показано на рисунке 3.8 и рисунке 3.9. Обобщенной жесткости.Откуда имеем
являющаяся эквивалентом жесткости контактной подвески соеденены параллельно,как это показано на рисунке 3.8 и рисунке 3.9. Обобщенной жесткости.Откуда имеем  =6,160*
=6,160*  Н/м.(Пружина 2 каретки не учитывается,т.к. ее развернутая длина мала и она введена для предотвращения ударов полоза токоприемника об узел верхнего шарнира).
Н/м.(Пружина 2 каретки не учитывается,т.к. ее развернутая длина мала и она введена для предотвращения ударов полоза токоприемника об узел верхнего шарнира).
Примем за обабщенный метод координаты вертикальные смещения тел из положения равновесия  и
и 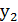 .
.
Кинетическая энергия системы равна:
Т=  (3.45)
(3.45)
Потенциальная энергия равна сумме потенциальных энергий деформированных пружин  и потенциальной энергии рассматриваемых тел в поле сил тяжести
и потенциальной энергии рассматриваемых тел в поле сил тяжести  :
:
П=  .
.
Здесь:
 (3.46)
(3.46)
где  и
и  статистическая деформация пружин при заданном контактном нажатии 100Н.
статистическая деформация пружин при заданном контактном нажатии 100Н.
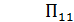 =
= 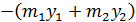 g, (3.47)
g, (3.47)
где g=9,8м/с  ускорение свободного падения.
ускорение свободного падения.
Как известно,условия равновесия определяется выражениеми:
 =0
=0
Из последних трех соотношений окончательно получаем:
П= 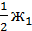 (
( 2
2 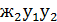 +
+ 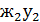 ² (3.48)
² (3.48)
Уравнения Лагранжа для рассматриваемой системы имеет вид:
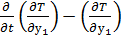 =
= 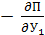 ;
;  =
= 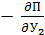 (3.49)
(3.49)
Подставляя (3.41) (3.48) в (3.49) получаем диффернециальные уравнения свободных колебаний в виде:
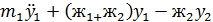 =0 (3.50)
=0 (3.50)
 +
+  =0 (3.51)
=0 (3.51)
Частные решения этих однородных дифференциальных уравнений с постоянными коэффициентами имеют вид:
 sin
sin  (3.52)
(3.52)
 sin
sin  (3.53)
(3.53)
где  и
и  амплитуды колебаний.
амплитуды колебаний.
Обозначим отношения обобщенных координат через  :
:
 =
=  =
= 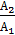 (3.54)
(3.54)
Тогда:
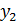 =
= 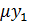 =
= 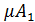 sin
sin  (3.55)
(3.55)
Подстановка (3.52) и (3.55) в систему уравнений (3.50), (3.51) дает после преобразований:
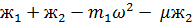 =0
=0
(3.56)
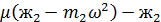 =0.
=0.
Исключая из последних соотношений параметр  получаем уравнения частот:
получаем уравнения частот:
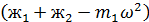 *
* 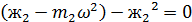 (3.57)
(3.57)
Преобразуя,получаем:
 +
+  = 0.
= 0.
Отсюда следует формула для вычисления частот главных колебаний рассматриваемой механической системы
 =
= 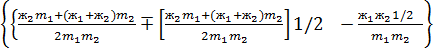 (3.58)
(3.58)
Подставляя из таблицы 3.3 численные значения величин,получаем главные частоты колебаний системы контактная-подвеска в середине пролета и у опор.Из таблицы 3.4 видно,что главные частоты колебаний системы токоприемник-контактная подвеска зависят от приведенной массы контактной подвески  .
.
Таблица 3.4-Характеристика главных колебаний системы токоприемник-контактная подвеска
У опоры
 =320Н/м =320Н/м
| В середине пролета
 220Н/м 220Н/м
| |||
 =40кг =40кг
|  =55кг =55кг
|  =30кг =30кг
|  =45кг =45кг
| |
 ,рад/с ,рад/с
| 3,346 | 3,382 | 3,605 | 3,314 |
 ,рад/с ,рад/с
| 12,66 | 11,913 | 16,94 | 16,0 |
 , Гц , Гц
| 0,533 | 0,618 | 0,574 | 0,527 |
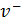 , Гц , Гц
| 2,01 | 1,897 | 2,700 | 2,545 |
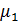
| 1,12 | 1,09 | 1,107 | 1,12 |

| 0,049 | 0,173 | -0,878 | -0,654 |

| -0,0513 | -0,2056 | -4,2445 | 1,642 |
При данной массе токоприемника частоты меняются с переходом от опорык середине пролета при этом основная,меньшая частота варьируется в интервале 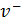 =0,527…0,618Гц,имея средние значения
=0,527…0,618Гц,имея средние значения 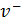 =0,563Гц,имея среднее значение
=0,563Гц,имея среднее значение 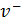 =0,563Гц,вторая частота варьеруется в пределах
=0,563Гц,вторая частота варьеруется в пределах  =1,897…2,700Гц,имея среднее значение
=1,897…2,700Гц,имея среднее значение  =2,288Гц
=2,288Гц 
Подставляя в любое (например,первое) уранения системы (3.56) полученные значения пары частот  и
и 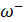 соответствующему каждому изглавных колебаний системы находим отвечающие ей два значения безразмерного коэффициента распределения
соответствующему каждому изглавных колебаний системы находим отвечающие ей два значения безразмерного коэффициента распределения  :
:
 =
= 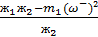 ; (3.59)
; (3.59)
 =
= 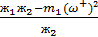 ;
;
Эти величины показывают во сколько раз амплитуда колебаний второго тела (полоз токоприемника вместе с контактным проводом) отличается от амплитуды колебаний первого тела(рам токоприемника) при первом и втором главных колебаниях.
На рисунке 3.10 представлены формы главных колебаний рассматриваемой системы токоприемник-контактная подвеска у опоры и в середине пролета. По горизонтальной оси отложены отклонения от равновесного положения каждой массы из рассматриваемой системы тел.За единицу принята амплитуда колебаний точки токоприемника, с которой крепятся рессорные пружины полоза.
У опоры В середине
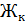 =320Н/м
=320Н/м 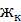 =220Н/м
=220Н/м

Р=Нsin(Pt+ 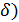
Рисунок 3.10 Формы главных колебаний системы: токоприемник с подрессоривание полоза и контактной подвески
Результирующие колебательное движения тел,образующих систему токоприемник-контактная подвеска описывается системой уравнений:
 =асоs
=асоs  t+bsin
t+bsin  t+
t+  cos
cos 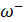 t+
t+ 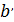 sin
sin 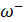 t, (3.60)
t, (3.60)
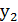 =
=  t+bsin
t+bsin  t)+
t)+  cos
cos 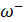 t+
t+ 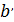 sin
sin 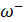 t), (3.61)
t), (3.61)
где 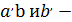 постоянные интегрирования, которые находятся из начальных условий. Эти амплитуды отличаются
постоянные интегрирования, которые находятся из начальных условий. Эти амплитуды отличаются  и
и  введенных в (3.52)
введенных в (3.52)
Конкретизируем задачу, например, следующими начальными условиями, они отвечают условиям нулевого контактного нажатия:
 (0)=h;
(0)=h;  (0)=0;
(0)=0; 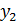 =(0)=0;
=(0)=0;  (0)=0, (3.62)
(0)=0, (3.62)
где h - постоянная определяющая начальное смещение рам токоприемника.
Подстановка (3.62) в (3.60) и (3.61) приводит к системе алгебраических уравнений:
 +
+  =0;
=0;  b+
b+  =0;
=0;  +b+
+b+ 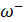 b=0;
b=0;  +
+  =h.
=h.
из которой следует, что:
b= 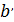 =0;
=0;  =
=  ;
;  =
= 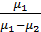 h. (3.63)
h. (3.63)
Подстановка (3.60) в (3.61) и (3.62) дает:
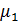 =
=  cos
cos  t +bsin
t +bsin  t+
t+  cos
cos 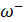 t+
t+ 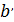 sin
sin 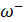 t (3.64)
t (3.64)
 =
= 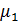 (
( cos
cos  t+ bsin
t+ bsin  t)+
t)+  (
( cos
cos 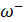 t+
t+ 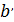 sin
sin 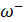 t) (3.65)
t) (3.65)
Для описания колебательных процессов в контактном проводе можно ограничиться рассмотрением только уравнения (3.61) другое уравнение (3.62)описывает колебания нижнего узла (рам) токоприемника
Обозначим в (3.63) коэффициент, перед скобками взятый с обратным знаком через G, он показывает зависимость амплитуды колебаний полоза, в контакте с проводом от коэффициентов распределения:
G=  . (3.66)
. (3.66)
Численные значения G легко получить из таблицы 3.4. Преобразуем к виду:
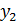 (t)=2Gsin
(t)=2Gsin  t*sin
t*sin  t (3.67)
t (3.67)
Введем две характерные частоты колебания высокую:
 =
=  (3.68)
(3.68)
и низкую:
 =
=  (3.69)
(3.69)
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 378; Нарушение авторских прав?; Мы поможем в написании вашей работы!