Введение. Целью курсовой работы является изучение и самостоятельное применение основных положений классической теории автоматического управления в решении задачи

Целью курсовой работы является изучение и самостоятельное применение основных положений классической теории автоматического управления в решении задачи электропривода – анализе системы автоматизированного электропривода постоянного тока и синтезе последовательного корректирующего устройства. Настоящая работа рассматривает задачи анализа и синтеза линейных непрерывных систем, а также отдельные приложения теории линейных импульсных (цифровых) систем управления. В качестве основного метода исследования используется метод логарифмических частотных характеристик (ЛАЧХ), который отличается простотой, наглядностью и приводит к легко обозримым результатам. Это позволяет применить его наряду с методами, основанными на использовании вычислительной техники, которые также используются в ходе выполнения работы.

Задача проектирования последовательного корректирующего устройства САУ состоит в том, чтобы на основании некоторых сведений об объекте управления и заданным техническим требованиям к системе в целом, рассчитать регулятор скорости, проверить его реакцию на различные возмущающие воздействия и помехи, выбрать соответствующую элементную базу, сконструировать регулятор, провести необходимые испытания и качественную наладку системы в целом, чтобы обеспечить хорошее качество регулирования.

1. Синтез последовательного корректирующего устройства – регулятора скорости (РС)

1.1. Определение передаточной функции неизменяемой части:

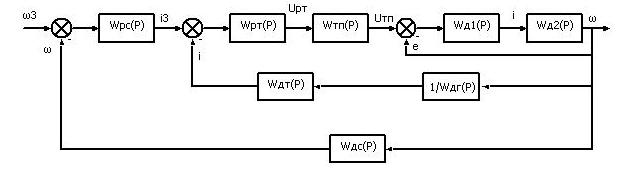
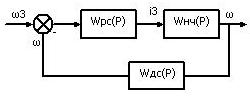
Рис. 3. Преобразование структурной схемы системы автоматического регулирования

W _рс(р) – передаточная функция регулятора скорости; W _нч(р) – передаточная функция неизменяемой части, включающая звенья, входящие в замкнутый контур тока, т.е. W _рт(р), W _тп(р), W _д1(р), W _дт(р), и звено объекта управления W _д2(р).

Определяем передаточную функцию неизменяемой части W _нч(р):

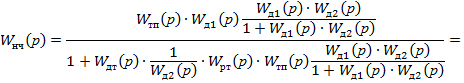
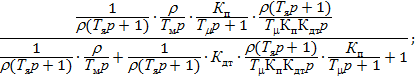
После алгебраических преобразований получим:

Подставим заданные значения в передаточную функцию неизменяемой части W _нч(р):

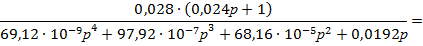
Определим полюсы передаточной функции неизменяемой части W _нч(р), предварительно выделив изодромное звено. Получим:

Затем, решая кубическое уравнение 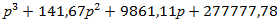= 0 получим следующие корни:

р₁ =-54,279; р₂ = -43,696+ i 56,64198; р₃ = -43,696- i 56,64198

Далее разобьем передаточную функцию на отдельные звенья:

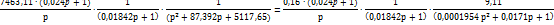
В итоге передаточная функция неизменяемой части W _нч(р) выглядит следующим образом

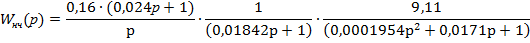
1.2. Построение частотных характеристик объекта регулирования (неизменяемой части системы):

Передаточная функция неизменяемой части представлена в виде произведения передаточных функций трех типовых звеньев: изодромного, апериодического и колебательного. Построив ЛАЧХ каждого звена и просуммировав их, получим ЛАЧХ неизменяемой части.

– изодромное звено, где: k₁=0,16; T₁=0,052 с; ω₁=19,23рад/с;

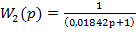–апериодическое звено, где: k₂=1; T₂=0,01842 с; ω₂=54,29рад/с;

W₃(p)= 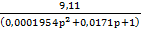– колебательное звено, где: k₃=9,11; T₃=0,01398 с; ω₂=71,53рад/с; ξ=0,6117;

Построения частотных характеристик выполняются в диапазоне от 1 до 1000 с^-1. Для построения характеристик были выбраны рекомендуемые масштабы: по частоте – 1 декада на 100 мм; по усилению – 10 дБ на 10 мм; по фазе - 90^° на 30 мм.

Для построения фазовых частотных характеристик выбираем частоты w в диапазоне [1с^-1 ¸1000 с^-1] , а также приведем формулы, по которым строятся ЛФЧХ для данных звеньев:

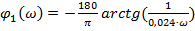- ЛФЧХ изодромного звена;

- ЛФЧХ апериодического звена;

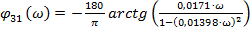- ЛФЧХ колебательного звена для частот ω<1/T;

- ЛФЧХ колебательного звена для частот ω>1/T;

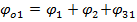– ЛФЧХ неизменяемой части для частот ω<1/T;

– ЛФЧХ неизменяемой части для частот ω>1/T;

- ЛФЧХ регулятора скорости;

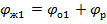– ЛФЧХ неизменяемой части при ω<1/T;

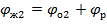– ЛФЧХ неизменяемой части при ω>1/T;

. – Рассчет ЛФЧХ

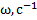
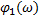
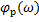
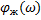
		-88,6252	-1,05527	-0,97985	-90,6603	-84,2894	-174,95
		-83,1572	-5,2621	-4,91078	-93,3301	-63,4349	-156,765
		-76,5043	-10,4369	-9,89337	-96,8345	-45	-141,835
	15,7	-69,3536	-16,1296	-15,7515	-101,235	-32,4948	-133,729
		-46,1691	-36,3828	-44,8623	-127,414	-14,0362	-141,45
		-34,7778	-47,8608	-73,8858	-156,524	-9,46232	-165,987
		-27,512	-55,8388	79,61039	-3,7404	-7,12502	-10,8654
		-22,6199	-61,503	60,83276	-23,2901	-5,71059	-29,0007
		-9,46232	-77,7481	20,8661	-66,3444	-2,29061	-68,635
		-8,77274	-78,6311	19,21425	-68,1896	-2,1211	-70,3107
		-4,76364	-83,8032	10,12879	-78,4381	-1,14576	-79,5838
		-3,17983	-85,8599	6,714553	-82,3251	-0,7639	-83,089
		-2,38594	-86,8925	5,025929	-84,2525	-0,57294	-84,8255

ЛАЧХ и ЛФЧХ объекта регулирования представлены на рис.4

1.3. Построение желаемой частотной характеристики разомкнутой системы и синтез корректирующего устройства:

Частота среза желаемой ЛАЧХ разомкнутой системы определяется по формуле:

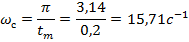
Граница первой низкочастотной области вычисляется по заданным показателям качества и имеет вид:

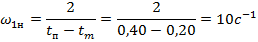
Низкочастотная часть желаемой ЛАЧХ обуславливает точность воспроизведения управляющего воздействия. Форма характеристики в этом диапазоне ω ϵ (0; ω_1н=10с^-1) зависит от требуемого порядка астатизма.

ЛАЧХ последовательного корректирующего устройства находится как разность желаемой ЛАЧХ Wж(р) и ЛАЧХ неизменной части Wнч(р), затем определяется передаточная функция регулятора W_PC(p). Желаемая ЛАЧХ и ЛФЧХ разомкнутой системы представлены на рис. 4.

Передаточная функция регулятора скорости имеет вид:

,

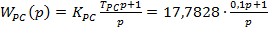где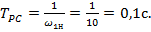

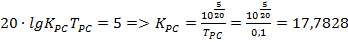
Передаточная функция желаемой ЛАЧХ имеет вид:

1.4. Анализ качества по реакции системы на ступенчатое управляющее воздействие:

С помощью программы Matlab (в частности, Simulink) оцениваю показатели качества полученой системы при ω_з(t)=1(t) и i_c(t)=0:

Рис.5. Структурная схема САР

1) перерегулирование ϭ= (30-50)%,

2)время достижения максимума t_m= c ϵ (0,15-0,2)c,

3)время переходного процесса t_п= c ϵ (0,3-0,4)c.

Спроектированная система обеспечивает заданные показатели качества переходного процесса, изображенного на рис. 6.

Рис.6. Реакция системы регулирования скорости ω(t) при ω_з(t)=1 и i_с(t)=0, N(t)=0.

Дата добавления: 2015-08-31