Описание и уравнения системы

Исходные данные

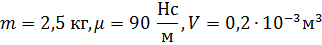
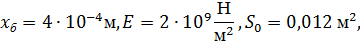
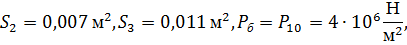
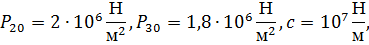
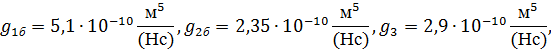
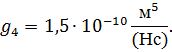
Принципиальная схема уплотнительного устройства приведена на рисунке 1. Основным конструктивным элементом устройства является плавающее кольцо 1, перемещение которого в осевом направлении x определяет величину торцового зазора Ι. При случайном изменении некоторого стационарного положения кольца возникают гидроупругие силы, приводящие к восстановлению этого положения. Например, при увеличении торцового зазора увеличивается давление в камере 2, при этом кольцо начинает двигаться влево, автоматически уменьшая зазор. Уплотнение рассчитывается таким образом, что равновесные состояния в обычных рабочих режимах имеют место при весьма малых зазорах. В результате обеспечивается требуемое качество уплотнения в условиях бесконтактной работы.

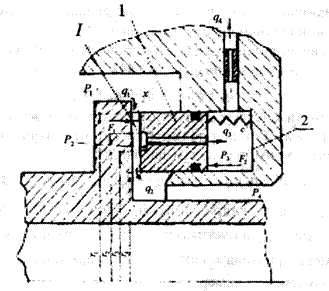
Рисунок 1

Уравнение динамики торцового уплотнительного устройства описывает движение кольца 1 в осевом направлении и гидродинамические процессы дросселирования рабочей жидкости.

Уравнение движение кольца имеет вид:

где - масса кольца; - коэффициент вязкого трения; 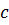- жесткость прижимающей пружины; 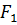- сила, раскрывающая зазор; 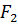- сила, закрывающая зазор; 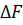- случайное возмущающее действие.

Уравнение гидростатических процессов составляются на основе баланса расходов (рис. 1):

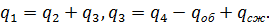
В данной системе допустимо считать режим течения ламинарным. Тогда расходы будут пропорциональны соответствующим перепадам давлений:

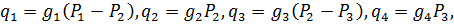
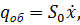где – гидравлические проводимости; давление внешней среды допустимо положить равным нулю. Расход на изменение расхода в камере 2 где 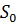– площадь торцового сечения камеры.

Расход на сжатие пропорционален скорости изменения давления в камере 2:

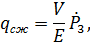
где 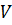- объем камеры; 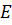- модуль упругости жидкости. Гидравлические сопротивления 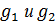пропорциональны кубу относительного зазора :

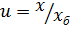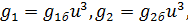
где 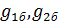- проводимости при номинальном режиме, определяемом зазором .

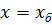С учетом выражений для расходов и сопротивлений уравнения балансов расходов примут вид:

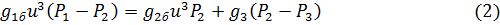
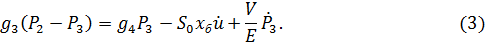
Выражения для раскрывающей и закрывающей зазор сил представляют собой линейные зависимости от соответствующих давлений:

где 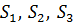- некоторые эквивалентные площади, расчет которых зависит от эпюр распределения давлений в торцовом зазоре.

Система, состоящая из линейного дифференциального уравнения (1), нелинейного алгебраического соотношения (2), линейного дифференциального уравнения (3) и линейных зависимостей (4), (5), полностью описывает статику и динамику уплотнительного устройства. Коэффициенты этих уравнений 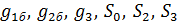задаются как исходные.

Для исследования устойчивости и динамики системы в малом отклонении, линеаризуем ее уравнения в области стационарного режима 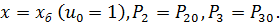Между стационарными значениями параметров должны выполняться, в силу исходных уравнений, соотношения:

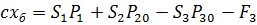
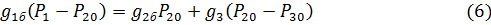
После записи линеаризованных уравнений для малых отклонений 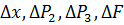и перехода к безразмерным переменным путем подстановки 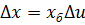, , 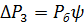, 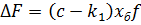получим уравнение системы в следующей операторной форме:

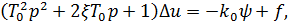
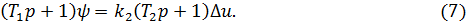
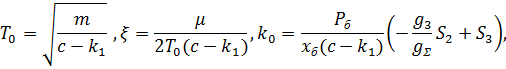
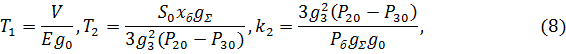
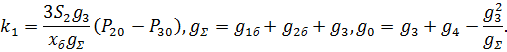
В качестве базисного давления примем .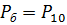

Дата добавления: 2015-08-31