Выполнение

I. Из исходной системы уравнений (1) – (5) получим линеаризованные в безразмерных отклонениях (7).

Рассмотрим соотношение между стационарными параметрами (6). Выражая давление 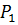, и подставляя полученное выражение в уравнение баланса расхода (2), получаем следующее выражение для давления :

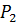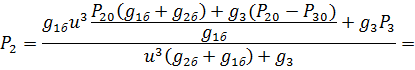
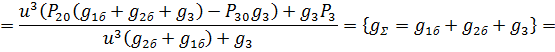
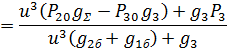
Подставляя данное выражение в соотношение (3), получаем:

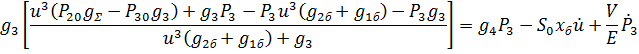
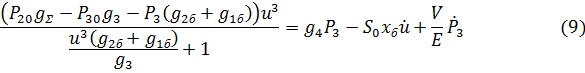
Стационарный режим:

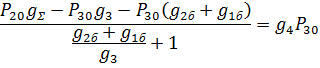
Линеаризуем уравнение (9) в области малых отклонений:

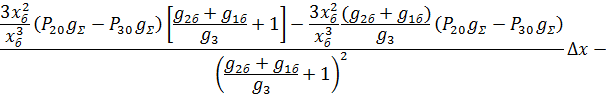
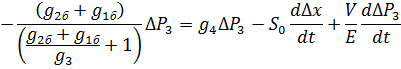
После преобразований получаем:

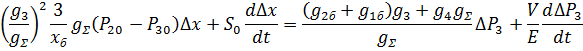
Перейдем к безразмерным переменным путем подстановки:

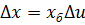
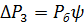
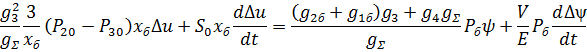
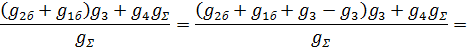
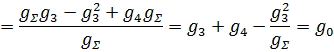
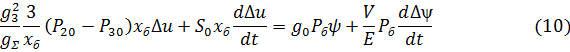
Выражение (10) представим в виде:

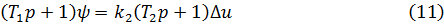
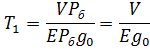
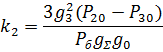
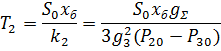
Линеаризуем уравнение (1):

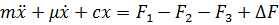
Так как:

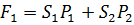
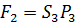
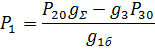
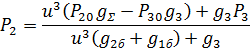
То, подставляя выражения для сил и давлений в уравнение (1), будем иметь:

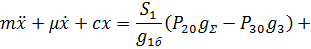
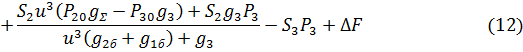
Стационарный режим:

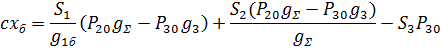
Линеаризуем уравнение (12) в области малых отклонений:

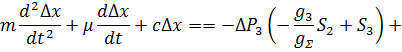
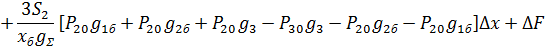
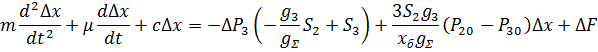
Перейдем к безразмерным переменным путем подстановки:

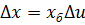
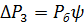
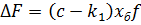
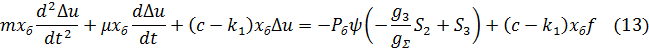
Где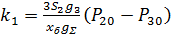

Представим (13) в виде:

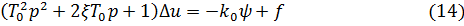
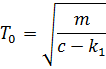
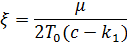
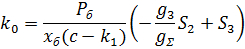
Как видим, (11) и (14) с системой линеаризованных уравнений (7).

II. Составим структурную схему.

Структурная схема представлена на рисунке 2:

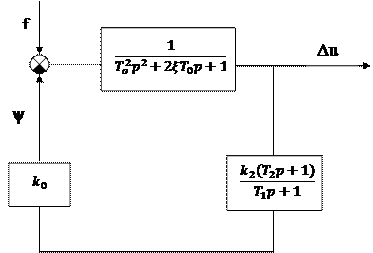Рисунок 2

III. Определим передаточную функцию замкнутой системы, запишем дифференциальное и характеристическое уравнения.

Передаточную функцию замкнутой системы найдем по формуле:

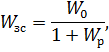
где 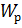– передаточная функция разомкнутой системы, 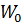– передаточная функция объекта.

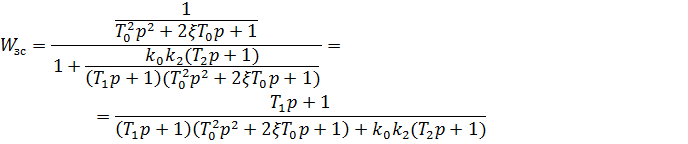
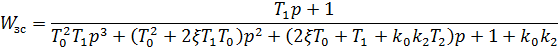
Характеристическое уравнение будет иметь вид:

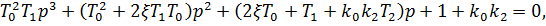
где p – характеристическое число.

Получим дифференциальное уравнение замкнутой системы:

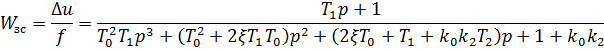
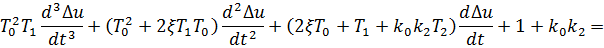
(15) - дифференциальное уравнение замкнутой системы.

IV. построим область устойчивости в плоскости параметров 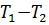и оценим запас устойчивости.

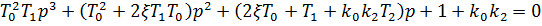
Для анализа устойчивости данного полинома составим определитель Гурвица:

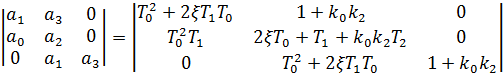
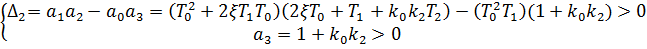
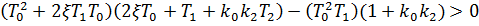
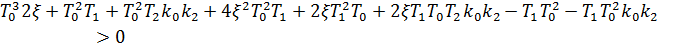
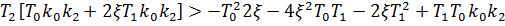
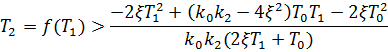
Область устойчивости, построенная в координатах 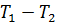, при заданных значениях параметров приведена на рисунке 3.

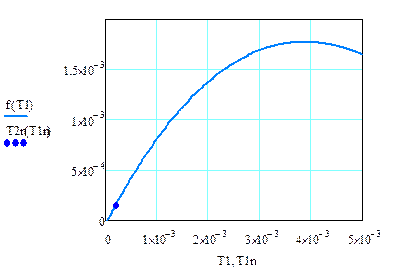
Рисунок 3

Для исходных 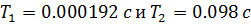рабочая точка лежит в устойчивой области, причем данное значение 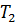превышает граничное по устойчивости значение 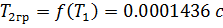в 686 раза.

V. сделаем выводы о влиянии конструктивных параметров (объема камеры V и площади торцового сечения кольца 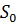) на устойчивость.

Характер граничной кривой области устойчивости (рис.3) показывает, что для обеспечения надежной устойчивой работы уплотнения следует по возможности увеличить площадь торцового сечения камеры 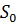(которой пропорциональна постоянная времени 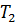) и предусмотреть возможно меньший объем камеры 2 (которому пропорциональна постоянная времени ).

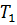VI. Вычислим и построим переходную характеристику h(t); определим время затухания процесса 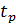из условия, что при 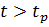будет .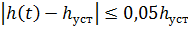

Положив 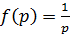, запишем изображение переходной характеристики

.

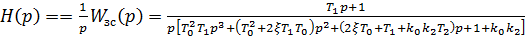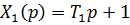
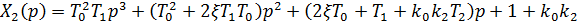
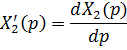
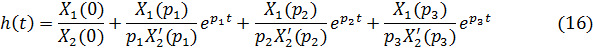
В формуле (16) - 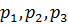- корни уравнения:

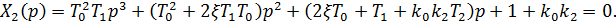
Построенная в среде Mathcad переходная характеристика (16) представлена на рисунке 4, 5.

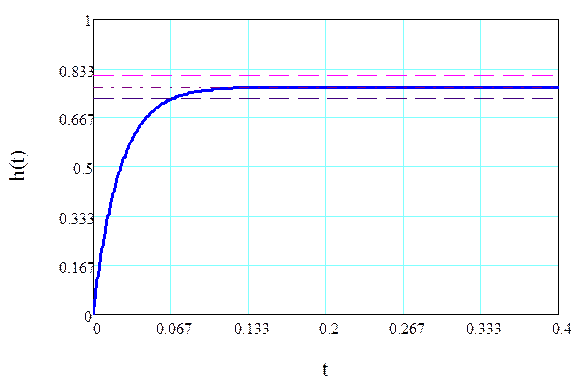
Рисунок 4

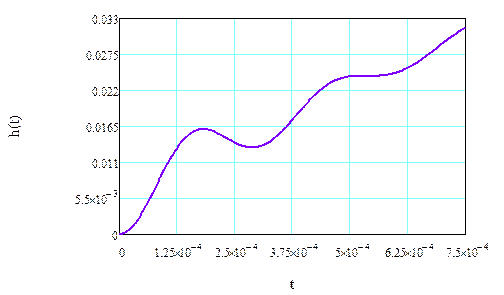
Рисунок 5

Определим время затухания :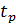

С рисунка 4: .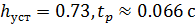

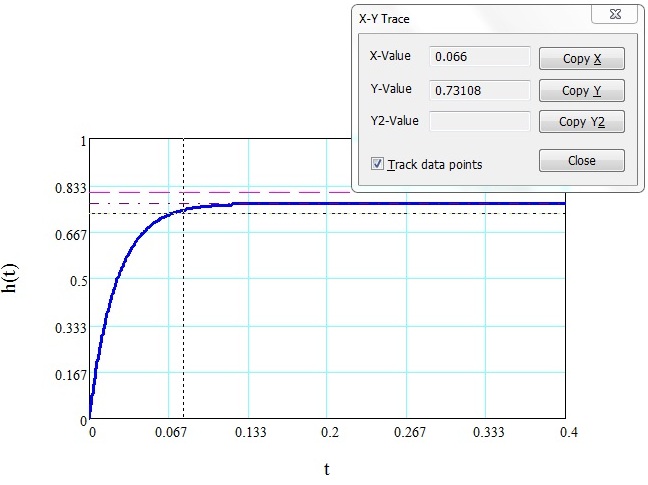
Рисунок 6

VII. Получим амплитудную характеристику.

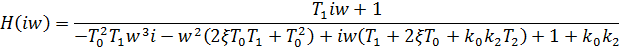
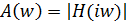
На рисунке 7 представлена амплитудная характеристика A(w).

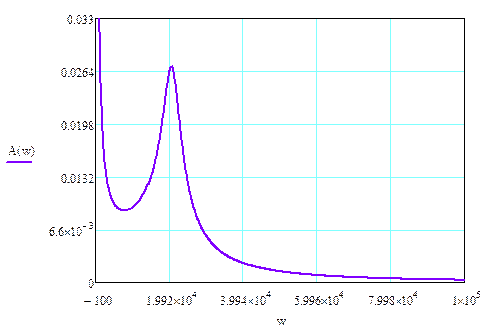
Рисунок 7

Дата добавления: 2015-08-31