Описати суть трансформації координат методом Гельмерта

РОЗДІЛ 6.ТРАНСФОРМАЦІЯ КООРДИНАТ МЕТОДОМ ГЕЛЬМЕРТА

Трансформацію координат можна виконати, якщо відомі координати пунктів в обох системах або параметри (“ключі”) переходу. Існує декілька способів розв’язку задачі для кожного з яких необхідна мінімальна кількість вихідних пунктів. Розв'язок буде найбільш достовірним якщо таких пунктів буде більше, що дозволить виконати трансформацію за методом найменших квадратів і оцінити точність отриманих результатів. Трансформація може бути виконана наступними способами:

1. Перетворення методом Гельмерта, при цьому ні кути, ні довжини сторін не деформуються

2. Афінне перетворення, можуть деформуватися і кути і лінії.

В першому випадку перетворення відбуваються зі збереженням масштабу.

Ми розглянемо перетворення двовимірних координат, тому що в сфері землеустрою це завдання виникає найчастіше.

Рис. 6.1.

Два різних набори планових геодезичних координат містяться у векторах 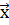та . Двовимірне перетворення подібності Гельмерта описується формулою:

(6.1)

де μ – масштабний множник;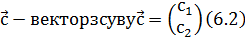

– матриця повороту (6.3)

Рівняння (6.1) в поєднанні з формулами (6.2) і (6.3) є двовимірним перетворенням Гельмерта з чотирма параметрами, зокрема двома компонентами зсуву с₁ та с₂, масштабним множником μ, а також кутом повороту 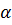. Підстановка рівняння (6.2) і (6.3) у вираз (6.1) дає формули для розрахунку координат точок:

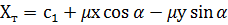
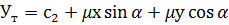(6.4)

Якщо параметри перетворення 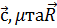відомі то за їх допомогою рівняння (6.4) координати з системи можна перетворити в систему . У випадку якщо параметри не відомі, то їх можна визначити використовуючи координати двох спільних точок, застосовуючи допоміжні невідомі:

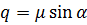(6.5)

Можна записати лінійне рівняння відносно невідомих:

Розглянувши систему цих рівнянь можна зробити висновок, що достатньо мати координати двох точок для розв'язку системи:

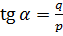(6.8)

Для визначення значень невідомих параметрів достатньо мати координати трьох точок в початковій і кінцевій системі координат, або ж параметри переходу.

Формули Гельмерта використовують в тих випадках, коли локальна мережа при трансформації координат її пунктів в іншу систему координат зберегла свої початкові форму і розміри. Це дуже важливо в тих випадках, коли існують юридичні документи на земельну ділянку (державний акт).

Дата добавления: 2015-08-31