Выявление лучшей модели. Значимость модели проверяем с помощью показателя Значимость F (ячейка F33) – вероятность неадекватности модели

Адекватность модели

Значимость модели проверяем с помощью показателя Значимость F (ячейка F33) – вероятность неадекватности модели. Оцениваем общее качество полученной модели: её достоверность по уровню значимости критерия Фишера. Мы рассчитаем его 1-Значимость F =1- 1,01641958321435= 0,01641958321435 отсюда следует, что уравнение регрессии значимо и применимо четырехфакторная модель для прогнозирования. Значимость отдельных коэффициентов а₀,а₁….. оценивается с помощью показателя t­-статистика, в основном на t-критерии Стьюдента диапазон ячеек «B-F» - вероятность отклонения фактора при построении модели. Результат записываем в строку под номером 4 таблицы Оценка. Столбец. Имеет ли значимость модель ставим «нет» только в том случае если в столбцах B-F стоит Да. Заполняем столбцы таблицы Стандартная ошибка, Множественный R переносим значения ячеек полученной таблицы Регрессионная статистика. (см. Приложение E)

Определяем переменную, которую следует вывести из модели. Для этого рассчитываем парные коэффициенты корреляции – меню Данные, Анализ данных, Корреляция, заполняем, как показано на рис 2, нажимаем Ок.

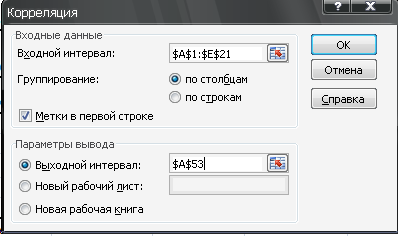Рис 2

После заполнения результат должен получиться следующим:

	y - доходы, тыс Руб	X1 - издержки	Х2 - штрафы и поощрения	Х3 - кол-во учеников	Х4 - кол-во проведенных часов
y - доходы, тыс Руб
X1 - издержки	-0,007729174
Х2 - штрафы и поощерения	0,23369941	-0,07286666
Х3 - кол-во учеников	-0,10387952	-0,180291903	-0,103704991
Х4 - кол-во проведенных часов	0,348653656	-0,030329301	-0,199977388	0,109003526

Среди частных коэффициентов корреляции между факторными признаками находим наибольшее значение по модулю, выделяя соответствующие факторные признаки. Для нашей модели это значение 0,199977388. Это означает, что факторные признаки штрафы и поощрения и кол-во проведенных часов сильно коррелируют между собой и один из этих признаков необходимо вывести из рассмотрения. По первому столбцу таблицы корреляция определяем коэффициенты корреляции этих факторов с результативным признаком Доход. Из рассмотрения следует вывести факторный признак штрафы и поощрения, так как коэффициент корреляции равный 0,23369941меньше чем 0,348653656 для факторного признака Объем производства. (см. Приложение А)

Переходим к построению трехфакторной линейной модели, для этого мы переименовали Лист Excel в Модель 3, копируем таблицу исходных данных, удаляем столбец - штрафы и поощрения. Уравнение регрессии y=15,82-0,001X₁-0,243X₃+0,088X₄. После расчетов трехфакторной модели факторные признаки издержки и количество учеников сильно коррелируют между собой и один из этих признаков необходимо вывести из рассмотрения. Выводим из рассмотрения факторный признак X₁ издержки. (См. Приложение В). Переходим к построению двухфакторной модели для этого мы переименовали Лист Excel в Модель 2. После анализа регрессии уравнение имеет вид y=15,57-0,24X₃+0,088X₄. После расчетов двухфакторной модели факторные признаки Х₃ количество учеников и Х₄ - количество проведенных часов сильно коррелируют между собой. Из рассмотрения двухфакторной модели можно вывести факторный признак Х₃ количество учеников, так как коэффициент корреляции у этого признака меньше чем у признака Х₄ количество проведенных часов. (см. Приложение С). Строим однофакторную модель мы переименовали Лист Excel в Модель 1 с одним фактором Х₄ количество проведенных часов. После анализа регрессии уравнение регрессии имеет вид y=10,93+0,084X₄. (см. Приложение D). После анализа таблицы оценка (см. Приложение Е) можно сделать вывод, что лучшая модель из 4-х это однофакторная, у этой модели самый маленький коэффициент корреляции.

Дата добавления: 2015-08-31