Экстремум функции двух переменных

Производная в данном направлении. Градиент функции

Производная функции в точке в направлении вектора называется 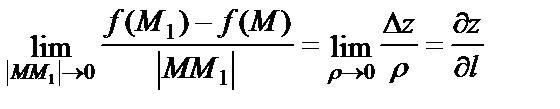, где .

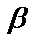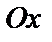Если функция дифференцируема, то производная в данном направлении вычисляется по формуле , где , - углы, образованные вектором с осями и 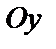. Производная по направлению 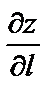дает скорость изменения функции 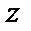в направлении вектора .

Градиентом функции в точке называется вектор, выходящий из точки 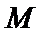и имеющий своими координатами частные производные функции :

;

.

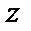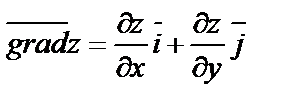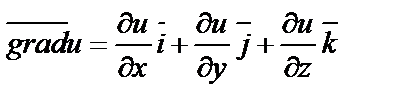Градиент функции и производная в направлении вектора связаны формулой . Градиент указывает направление наибыстрейшего роста функции в данной точке.

Пример 1. Вычислить производную функции в точке в направлении вектора и градиент.

Решение. Найдем значение частных производных в точке .

; .

Вычислим направляющие косинусы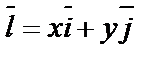

; .

Тогда:

;

;

;

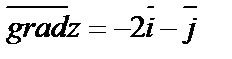
Функция имеет максимум (минимум) в точке , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке некоторой окрестности точки , то есть (соответственно ) для всех точек , принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума.

Необходимое условие экстремума: если дифференцируемая функция достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, то есть: , .

Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума.

Достаточное условие существования экстремума:

Пусть стационарная точка функции . Обозначим , , и составим дискриминант 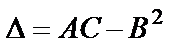. Тогда:

если , то функция имеет в точке экстремум, а именно максимум, при (или ) и минимум, при (или );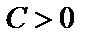

если , то в точке экстремума нет;

если , то требуется дальнейшее исследование (сомнительный случай).

Пример 1. Найти экстремум функции .

Решение. Находим частные производные первого порядка и и критические точки, в которых они равны нулю или не существуют: ; . Решая систему , найдем две точки: и . Обе точки являются критическими, т.к. функция определена на своей плоскости 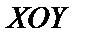. Исследуем критические точки и по знаку определителя , составленного из частных производных второго порядка: ; ; . Для точки получим 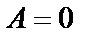, , . . Следовательно, согласно достаточному условию в точке нет экстремума.

Для точки получим , , ,

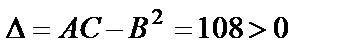. Согласно достаточному условию 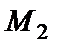есть точка минимума .

Функция , непрерывная в некоторой ограниченной замкнутой области , обязательно имеет в этой области наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри области , или в точках, лежащих на границе области.

Чтобы найти наибольшее (наименьшее) значение функции в ограниченной замкнутой области , где она непрерывна, можно руководствоваться следующим:

1. Найти критические точки, лежащие внутри области , и вычислить значения функции в этих точках (не вдаваясь в исследование, будет ли в них экстремум функции и какого вида).

2. Найти наибольшее (наименьшее) значение функции на границе области .

3. Сравнить полученные значения функции: самое большое (меньшее) из них будет наибольшим (наименьшим) значением функции во всей области .

Пример 2. Найти наибольшее и наименьшее значения функции в круге .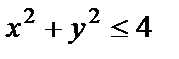

Решение. 1. Находим первые частные производные:

.

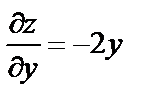
2. Найдем наибольшее и наименьшее значения функции на границе, то есть на окружности , то для точек окружности функцию можно представить как функцию одной переменной 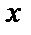: 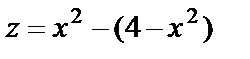, то есть , причем .

Найдем наибольшее и наименьшее значения этой функции. Находим критические точки функции в интервале 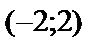и вычислим значения функции в этих точках и на концах интервалов: , .

Отсюда имеем критическую точку ; 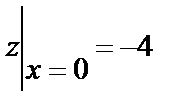. На концах интервала : ; .

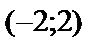3.Выпишем полученные значения функции:

, ,

Отсюда видим, что функция имеет наибольшее значение, равное 4, и наименьшее значение, равное –4.

Замечание. Если граница области определения функции состоит из нескольких частей, например, треугольник или прямоугольник, то находят наибольшее и наименьшее значения функции на каждой части, а затем сравнивают.

Дата добавления: 2017-01-13