Примеры использования формул теории вероятности для расчета надежности

1. Экспоненциальный закон распределения событий

Определить вероятность безотказной работы элемента конструк­ции технического средства в течении срока t=10000 часов, если зада­на интенсивность отказов λ=10^-8 1/час.

Решение.

Вероятность безотказной работы в этом случае определяется формулой

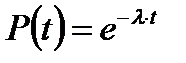
а если λ×t <0,1 можно использовать формулу

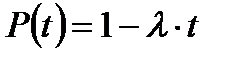
Определим λ×t=10^-8×10⁴=10^-4<0,1, тогда

P(t)=1-10^-4=0,9999.

2. Нормальный закон распределения событий

2.1. Определить вероятность безотказной работы элемента конст­рукции технического средства в течении t=1,5×10⁴ часов, если извест­но математическое ожидание безотказной работы этой детали t_m=4×10⁴ часов и среднее квадратическое отклонение этой величины S=10⁴ часов.

Решение.

По формуле подсчитаем квантиль нормализованного

нормального распределения

U_p=(1,5-4)×10⁴/10⁴=-2,5.

По табл. 1 нормализованного нормального закона находим, что квантилю U_p=-2,5 соответствует вероятность безотказной работы

P(t)=0,9938.

2.2. Определить ресурс работы элемента конструкции технического средства, обладающего следующими показателями надежности:

вероятность безотказной работы P(t)=0,8,

математическое ожидание безотказной работы этой детали t_m=10⁴ часов,

среднее квадратическое отклонение от математического ожида­ния S=6×10³ часов.

Решение.

По табл. 1 нормализованного нормального распределения опреде­ляем, что вероятности безотказной работы P(t)=0,8 соответствует квантиль U_р=-0,84. Тогда ресурс работы элемента конструкции техни­ческого средства, соответствующий вероятности безотказной работы P(t)=0,8, определится вышеприведенной формулой

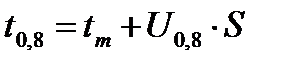
В результате имеем

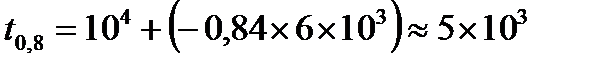(часов).

Заключение

Согласно выше изложенному тексту одной из основных характери­стик работоспособности технического средства является показатель надежности, определяемый вероятностью его безотказной работы P(t) в течение определенного срока службы t. Для определения этого по­казателя необходимо знание закона распределения случайной вели­чины t - времени наработки на отказ, который устанавливается в про­цессе сбора статистической информации по результатам подкон­трольной эксплуатации или специально организованных испытаний технического изделия. В про­цессе обработки этой информации используются методы и средства теории математической статистики: корреляционный и регрессионный анализы, методы статистического моделирования и методы оценки случайных функций, описанные в специальной литературе.

Задачи

1. Долговечность технического средства имеет нормаль­ное распределение с математическим ожиданием 5000 ча­сов и средним квадратическим отклонением 125 часов.

а) Постройте график плотности нормального распределения для дан­ного случая.

б) Определите значение плотности распределения в точке 3500 часов.

в) Определите ожидаемое количество технических средств, вышед­ших из строя за 2500 часов.

г) Определите вероятность безотказной работы технического средства в течение 4000 часов работы.

2. Испытаниям на долговечность подвергаются 15 одина­ковых устройств автомобилей коммунального хозяйства. Нара­ботка измеряется в тысячах часов. Отказы произошли при сле­дующих значениях наработки: 0,9, 1,5, 2,4, 3,4, 4,1, 4,5, 5,1, 5,5, 6,0, 6,7, 7,1, 7,7, 7,9, 8,3, 8,8 тысяч часов.

а) Постройте графики плотности распределения наработки до отказа, вероятности появления отказа, интенсивности отказов.

б) Предложите математическую модель интенсивности отказов.

3. Наработка элемента конструкции автомобиля до отказа подчиняется экспоненциальному закону распределения с интен­сивностью отказа Л =0,012 1/тыс. км. Требуется определить среднюю наработку до отказа ц, вероятность безотказной работы P(t) и плот­ность распределения вероятностей f(t) для наработки ^=30 тыс. км. и f₂=120 тыс. км.

4. Определить вероятность безотказной работы P(t) элемен­та металлоконструкции в течение f=10⁵ часов, если ресурс металлоконструкции описывается распределением Вейбулла с параметрами: a) t₀=1,5×10⁵, m=2,3; 6)t₀=10⁵, m=2,3; t₀=0,5×10⁵, m=2,3.

Дата добавления: 2017-01-13