Экстремумы и строение графика

Лекция № 14. 09. 12. 2016

Ряд Тейлора, метод его получения с помощью прогрессий.

Существует формула суммы бесконечной убывающей геометрической прогрессии .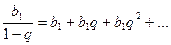

Но мы ведь можем вынести первый член прогрессии за скобку, а также и из числителя дроби, то есть привести к виду, чтобы прогрессия начиналась с единицы. Поэтому проще запомнить формулу в таком виде: .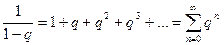

Пример. Разложить в степенной ряд в окрестности точки функцию .

Решение. Можем рассматривать в интервале то есть . Тогда .

Серия других примеров на применение прогрессий будет рассмотрена на практике.

Монотонность и знак производной.

Вспомним определение монотонного роста и убывания: если при 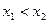выполняется 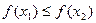, то функция монотонно возрастает, а если 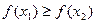то монотонно убывает. Рассмотрим, как монотонность взаимосвязана со знаком 1-й производной.

Лемма. 1) 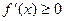тогда и только тогда, когда монотонно возрастает.

2) тогда и только тогда, когда монотонно убывает.

Доказательство. Рассмотрим функцию 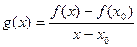(это та самая функция, которая была в определении предела).

Предел 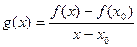при 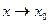это и есть .

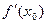Возьмём . Если f мнонтонно возрастает, то при этом , то есть дробь положительна. Если функция положительна, то и её предел больше нуля, тогда .

Аналогично, если функция отрицательна, то и её предел меньше нуля, тогда .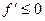

Определение 1 (точки наибольшего, наименьшего значения в D).

Пусть функция f - функция одной переменной, т.е. отображает некоторое множество в 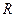. Точка 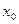называется точкой наибольшего (соответственно, наименьшего) значения в D, если 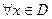. (соответственно, ).

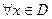Примечание. Здесь это область определения, может совпадать со всей числовой прямой, но не обязательно.

Определение 2. (максимум и минимум)

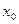Пусть функция . Точка называется точкой максимума (минимума), если существует окрестность точки 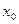, такая, что . (для минимума ).

Для максимума и минимума есть общее название - «экстремум».

Локальных максимумов в смысле определения 2 может быть несколько или даже бесконечное количество. Например, график , здесь через каждые есть новый максимум, который выше того, что слева от него:

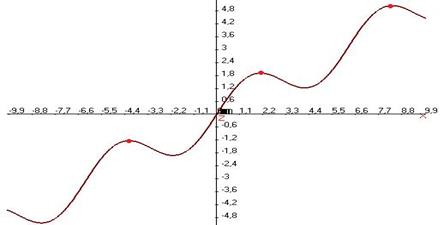
Понятие «максимум» отличается от понятия «наибольшее значение» тем, что для максимума требуется, чтобы функция была наибольшей в некоторой окрестности, а для наибольшего значения - во всей области.

Взаимосвязь между равенством нулю первой производной и экстремумом не однозначна. Так, функция имеет минимум в точке 0, но там не существует производная, то есть нельзя сказать, что . А для функции , , 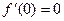но при этом нет экстремума.

Рассмотрим подробно структуру функции в случае, когда производная не равна 0.

Дата добавления: 2017-01-13