Вынужденные колебания

ЛЕКЦИЯ 12

ЛЕКЦИЯ 11

Гармонические колебания. Физический маятник.

Периодическое движение – через равные промежутки времени (период 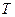) движение повторяется.

Гармоническое колебание материальной точки – координата точки изменяется по гармони-ческому закону

.

Здесь 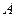- амплитуда колебания, 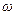- круговая (циклическая) часто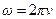та, , - частота, - фаза колебания, - начальная фаза.

Скорость материальной точки, совершающей гармоническое колебание:

.

Исодя из этого выражения, можно говорить, что при гармоническом колебании скорость опережает по фазе координату на .

Ускорение колебательного движения:

.

Таким образом, мы приходим к уравнению осциллятора

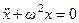, (1)

составлющему основу теории колебаний (производная обозначена точками).

Собственные колебания возникают за счет собственных сил, существующих в самой системе. Частота таких колебаний называется собственной частотой.

Пример. Пружинный маятник.

, . Значит собственная частота , .

Полная энергия материальной точки при гармонических колебаниях:

.

Средние за период значения кинетической и потенциальной энергии:

, .

Таким образом, при гармонических колебаниях

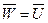(частный случай общей теоремы вириала).

Математический маятник – тело, подвешенное на невесомой нерастяжимой нити, размер которого намного меньше длины нити.

Физический маятник – тело, закрепленное на оси, расположенной выше центра масс.

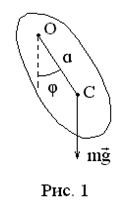
Основной закон вращательного движения для такого тела

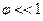(). Преобразуем его к виду (1)

.

Тогда , - период колебаний физического маятника.

Если размеры тела малы по сравнению с расстоянием 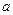(материаль-ная точка), то и мы приходим к известной формуле для периода математического маятника

.

Приведенная длина физического маятника – это длина математического маятника с тем же периодом колебаний, что и у физического. Приравнивая выражения для периодов, получим

.

Обозначим через точку, лежащую на продолжении отрезка 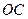и отстоящую от точки подвеса на расстоянии 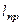. Точка называется центром качаний физического маятника. Можно показать, что физический маятник обладает следующим важным свойством: если физический маятник подвесить за центр качаний, то период его колебаний не изменится.

Затухающие и вынужденные колебания. Резонанс.

В любой колебательной системе со временем происходит затухание колебаний, обусловлен-ное потерей энергии под действием неконсервативных сил. Рассмотрим затухание колеба-ний материальной точки под действием силы вязкого трения (лекция 10)

.

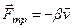В этом случае 2-ой закон Ньютона для материальной точки под действием возвращающей сил и силы трения в проекции на ось 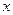можно представить в виде

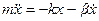. (1)

Коэффициент 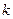необязательно должен иметь смысл коэффициента жесткости. Он может описывать возвращающую силу любой природы.

Можно показать, что при условии 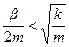решение уравнения (1) имеет вид

,

где - начальная амплитуда колебаний, 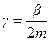- коэффициент затухания, - частота затухающих колебаний, - собственная частота.

Функция 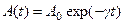представляет собой амплитуду затухающих колебаний (рис. 1). Для характеристики скорости затухания колебаний вводится логарифмический декремент затухания

.

Затухающие колебания существуют при выполнении условия . При имеет место апериодический процесс, при котором точка возвращается в положение равновесия, не совершив ни одного колебания.

Рассмотрим колебания материальной точки при наличии периодической внешней силы

,

действущей вдоль оси 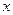. Уравнение движения в этом случае принимает вид:

, или в приведенном виде

. (2)

Уравнение (2) называется неоднородным дифференциальным уравнением 2 – го порядка, а уравнение (1) соответствующим ему однородным уравнением.

В теории дифференциальных уравнений доказывается следующая теорема.

Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения:

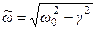, где . (3)

Частное решение неоднородного уравнения будем искать в виде:

. (4)

Следует отметить, что амплитуда 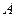и фаза в этом решении уже не определяются лишь начальными условиями как в свободных колебаниях, а зависят от параметров колебательной системы. Подставляя решение (4) в уравнение (2), можно получить следующие выражения для 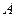и

, .

Общее решение уравнения (2) является суммой решений (3) и (4). При решение (3) станет пренебрежимо малым и установятся вынужденные колебания вида (4). По этой причине величина называется временем установления колебаний.

На рис. 2 приведена зависимость амплитуды вынужденных колебаний 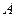от частоты вынуждающей силы 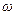. Амплитуда имеет максимальное значение при

.

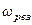Это явление резонанса вынужденных колеба-ний. С ростом коэффициента затухания реонансная частота и резонансная амплитуда уменьшаются. В отсутствие затухания (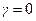) и . Физически это происходит из-за того, что в колебательную систему непрерывно поступает энергия за счет работы внешней силы, а потери энергии отсутствуют.

При амплитуда . Величина называется добротностью колебательной системы.

Дата добавления: 2017-01-13