Векторное произведение векторов

Прямоугольная (декартова) система координат

Базис. Координаты вектора

Пусть V – векторное пространство. Базисом в пространстве V называется всякая система векторов 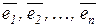, которая линейно независима и полна (т. е. всякий вектор пространства можно выразить через данную систему векторов).

Обозначим через V₁ – множество векторов на прямой; V₂ – множество векторов на плоскости; V₃ - множество векторов в пространстве.

Базисом в V₁ называется любой ненулевой вектор; в V₂ – любая пара неколлинеарных векторов; в V₃ – любая упорядоченная тройка некомпланарных векторов.

Теорема о разложении вектора по базису:Любой вектор можно разложить по базису единственным образом:

1) в V₁: ;

2) в V₂: ;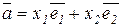

3) в V₃: .

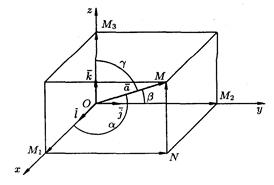
Системой прямоугольных (декартовых координат) называется совокупность точки O и базиса, обозначаемого 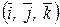и удовлетворяющего условиям:

1) =1;

2) ,

3) тройка векторов 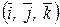- правая.

Любой вектор можно представить в виде разложения по базису

:

,

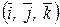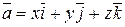числа х, у, z называются прямоугольными ( декартовыми ) координатами вектора .

Геометрический смысл координат вектора – координаты вектора есть проекции этого вектора на координатные оси:

х= ;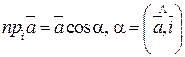

у= ;

z= .

Cos a, cos b, cos g - называются направляющими косинусами вектора.

Пусть даны точка М₁ (х₁,у₁,z₁) и точка М₂ (х₂,у₂,z₂), тогда вектор .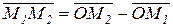

Координаты вектора .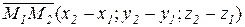

Модуль вектора , равный расстоянию между точками М₁ и М₂, находится по формуле:

.

Рассмотрим векторы (х_а; у_а; z_а) и (х_b; у_b; z_b), тогда

- если , то (х_а+х_b; у_а+у_b; z_а+z_b);

- если , то (l х_а; l у_а; l z_а).

Условие коллинеарности векторов в координатной форме:

векторы и коллинеарны ( =l ) тогда и только тогда, когда

.

Координаты середины отрезка М₁М₂:

.

2.7. Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними:

.

Алгебраические свойства скалярного произведения:

1) 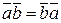- свойство коммутативности;

2) - скалярное произведение вектора на себя равно квадрату модуля вектора;

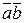3) ( a )= a () – свойство ассоциативности;

4) ( + ) = 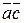+ - свойство дистрибутивности.

Геометрические свойства скалярного произведения:

1) тогда и только тогда, когда 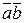= 0 – условие ортогональности векторов;

2) Два ненулевых вектора и составляют:

- острый угол, если >0;

- тупой угол, если <0;

Скалярное произведение в координатах двух векторов (х_а; у_а; z_а) и (х_b; у_b; z_b) есть число, равное сумме произведений одноименных координат:

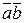= x_ax_b+y_ay_b+z_az_b.

Из определения скалярного произведения вытекают следующие формулы:

- косинус угла между векторами ;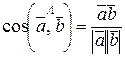

- проекция вектора на вектор равна .

Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:

1) ; (2)

2) ;

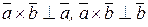3) тройка векторов , , - правая (кратчайший поворот от вектора к вектору происходит против часовой стрелки).

Алгебраические свойства векторного произведения:

1) 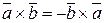- свойство антикоммутативности;

2) (a )´ = a () – свойство ассоциативности;

3) 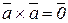- векторное произведение вектора на себя равно нулю.

Геометрические свойства векторного произведения:

1) вектора и коллинеарны, если = 0;

2) модуль векторного произведения | ´ | равен площади S параллелограмма, построенного на приведенных к общему началу векторах и - геометрический смысл векторного произведения.

Векторное произведение в координатах векторов (х_а; у_а; z_а) и (х_b; у_b; z_b) есть вектор, вычисляемый по правилу: .

Из определения векторного произведения вытекают следующие формулы:

- синус угла между векторами ;

- площадь треугольника, построенного на векторах и , равна 1/2| ´ |.

Дата добавления: 2017-01-13