Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Виды уравнений плоскости

Задание плоскости в пространстве

Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

Способ задания прямых	Угол между двумя прямыми	Условия параллельности	Условия перпендику-лярности
Прямые заданы общими уравнениями: , .
Прямые заданы каноническими уравнениями: , .
Прямые заданы уравнениями с угловым коэффициентом: ,

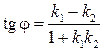
Плоскость в пространстве может быть задана:

1) тремя точками плоскости;

2) точкой и нормальным вектором плоскости, тогда множество точек М плоскости, проходящей через точку М₀ ортогонально вектору , будет удовлетворять условию .

3) точкой и двумя неколлинеарным векторам , , 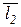тогда множество точек М плоскости будет удовлетворять условию, что векторы , , 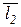компланарны

1) Общее уравнение плоскости:

Ах+By+Cz+D=0,

где (A;B;C) – нормальный вектор плоскости.

2) Уравнение плоскости,проходящей через точку М₀ параллельно

двум неколлинеарным векторам (m₁;n₁;p₁), 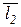(m₂;n₂;p₂).

.

2)

Уравнение плоскости, проходящей через три точки

М₁ (x₁;y₁;z₁), M₂ (x₂;y₂;z₂), M₃ (x₃,y₃,z₃):

.

Это уравнение есть условие компланарности трех векторов .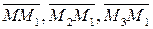

Пусть две плоскости p₁ и p₂ заданы общими уравнениями:

p₁: A₁x+B₁y+C₁z+D=0;

p₂: A₂x+B₂y+C₂z+D=0.

Вопрос об определении угла между указанными плоскостями сводится к определению угла j между их нормальными векторами 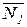(А₁,В₁,С₁) и (А₂,В₂,С₂).

Из определения скалярного произведения 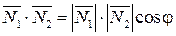и записи его в координатной форме, получим:

.

Условие параллельности плоскостей p₁ и p₂, эквивалентное условию коллинеарности векторов 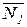(А₁,В₁,С₁) и (А₂,В₂,С₂), заключается в пропорциональности координат этих векторов, т.е. имеет вид:

.

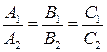Условие перпендикулярности плоскостей p₁ и p₂ выражается равенством нулю скалярного произведения векторов (А₁,В₁,С₁) и (А₂,В₂,С₂). Оно имеет вид:

А₁А₂+В₁В₂+С₁С₂=0.

Дата добавления: 2017-01-13