Доказательство. Пусть слово ведет в состояние представителя

Определение

Замечание

Доказательство.

Пусть слово ведет в состояние представителя . Покажем индукцией по длине слова 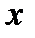, что . Для пустого слова утверждение очевидно (слово длины 0 есть пустое слово- оно соответствует начальному состоянию). Пусть утверждение доказано для слов длины не более , докажем его для слова длины Т.е. - слово 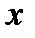имеет слово 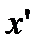длины 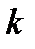началом и оканчивается на букву 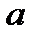. Пусть слово 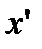ведет в состояние представителя 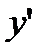. Тогда по предположению индукции .

Если к эквивалентным словам добавить любое, одно и тоже оканчание, то плученные слова также являются эквивалентными.

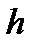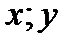Если предположить противное: , но при некотором получим не эквивалентные слова , тогда остаточные функции слов не равны, тогда слова не эквивалентны.

Таким образом, . Также по построению имеем .

По транзитивности отношения эквивалентности имеем .

Из доказанного непосредственно следует, что слова 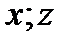ведут в одно и тоже состояние

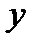, тогда и только тогда, когда они эквивалентны. Если 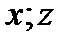ведут в одно и тоже состояние 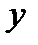, то по доказанному они эквивалентны , поэтому по транзитивности эквивалентны между собой. Пусть теперь 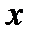ведет (по доказанному ), а ведет в другое состояние 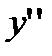(по доказанному 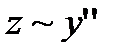) т.е. 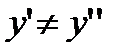. Предположив противное , получим 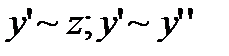). Противоречие. Утверждение доказано.

Основное утверждение корректности справедливо в силу замечания, и того факта, что слова ведущие в одно и тоже состояние автомата соответствуют одной и тойже остаточной функции.

7.2 Схемы автоматов.

Подобно конечным двоичным функциям, можно рассмотреть возможность представления автомата в виде схемы функциональных элементов. Отличие в том, что автомат имеет конечную память. Чтобы реализовать возможность памяти используется элемент задержки, выход которой в момент времени t+1 равен входу в предыдущий момент времени t, t=0…

Автомат однозначно определяется следующими итеративными соотношениями:

где – дискретное время , – начальное состояние автомата (соответствующее начальному моменту времени ),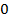

и 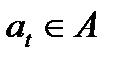– входные состояние и символ на ленте, 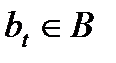– выходной символ автомата в момоент времени функционирования автомата.

Элементом задержкой называют автомат, который осуществляет следующее преобразование:

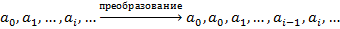
Т.о. выход автомата в момент времени 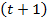является входом этого автомата в предыдущий момент времени . Это преобразование действительно автоматное, оно записывается следующими итеративными соотношениями ():

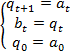
Постройте диаграмму автомата-задержки. Постройте диаграмму автомата-сумматора, который вычисляет сумму двух двоичных чисел (биты входных чисел считывать слева направо).

Рассмотрим базис из функциональных символов .

Функциональная схема в базисе определяется аналогично схеме из функциональных символов , , .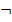

Схемой в базисе 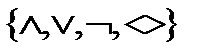на множестве входов , с множеством выходов называется ориентированный граф с возможными циклами, входам которого (вершины из которых нет входящих ребер) приписаны входные переменные 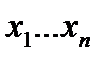, выходам которой (вершины, в которые нет выходящих ребер) приписаны выходные переменный , остальным вершинам приписаны функциональные элементы базиса , причем в каждом цикле есть хотябы один элемент задержки.

Замечание. В схеме, однако, допускаются циклы, но каждый цикл обязательно содержит хотя бы одну задержку.

Например, схема на рисунке имет входы– и выход – . Общая схема в рассмотренном базисе функционирует во времени..

Определение. Каждая схема в рассмотренном базисе реализует некоторую автоматную функцию следующим образом.

Рассмотрим произвольную схему в данном базисе. Пусть входам этой схемы приписаны переменные , а выходам переменные 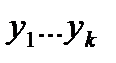. Также элементы задержки приписаны вершинам . Входы этих вершин приписаны вершинам . Далее в графе схемы удалим ребра, сосединяющие вершины с 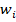(). Т.к. каждый цикл первоначального графа содержит хотя бы один элемент задержки, то получим после преобразования ациклический граф.

Объявим новыми входами схемы и припишем им входные переменные , а вершины 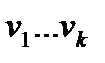объявим новыми выходами схемы, и припишем им переменные . Новые входы и выходы находятся во взаимно однозначном соответствии. Выходной переменной будет соответствовать входная переменная . Т.к. получена схема из функциональных элементов , то она определяет некоторый двоичный оператор. Выход есть двоичная функция от входных переменных .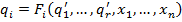

Точно так же . есть некоторая функция от входных переменных. Естественно считать, что преобразование одномоментное, т.е. все преобразования производятся в один и тотже момент времени.

Теперь возвратимся к начальной схеме вычислений, т.е. восстановим элементы задержки выходного элемента задержки в момент времени . . Заменяя соответствующие переменные на , получаем автоматное преобразование:

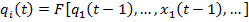
Это и есть функциональное определение автомата.

Утверждение. Для каждой ограниченно-детерминированной функции существует схема в базисе , которая реализует данную автоматную функцию.

Рассмотрим некоторое функциональное соотношение и построим схему, которая ее осуществляет. Не теряя общности будем считать, что алфавит входа и выхода . В противном случае можно перейти к алфавиту.

Рассмотрим соответствующие операторы и автомата как одномоментные выполнимые в один и тотже момент времени t. Это обычные двоичные операторы, каждый компонент которого – некоторая двоичная функция:

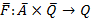, векторная функция размерности .

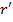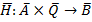, векторная функция размерности .

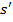Т.к. это обычные двоичные операторы, то мы их можем реализовывать обычной функциональной схемой . Изобразим это представление на рисунке.

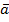
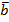
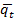
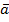
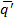
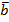
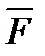
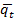
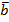
Схема слева реализует одномоментные операторы и : и . Введем задержку между входом 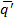и выходом . Когда вводится элемент задержки, то входные/выходные элементы связываются соотношением . Подставляя эти соотношения в предыдущие функции равенства, получаем искомую автоматную функцию: рисунок схемы справа.

Дата добавления: 2017-01-13