
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Критерий префиксного кодирования Мак-Миллана
|
|
|
|
Критерий префиксного кодирования Мак-Миллана.
Определение. Кодирование  называют типа
называют типа  , если существует
, если существует  штук кодовых слов единичной длины,
штук кодовых слов единичной длины, 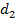 кодовых слов из двух букв,
кодовых слов из двух букв, 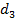 слов из трех букв, …,
слов из трех букв, …,  слов длины
слов длины 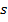 .
.
Критерий. Префиксное корректное кодирование типа  существует тогда и только тогда, когда
существует тогда и только тогда, когда

 – мощность кодирующего алфавита.
– мощность кодирующего алфавита.
Необходимость. Пусть 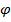 – корректное кодирование типа
– корректное кодирование типа  . Покажем справедливость формулы
. Покажем справедливость формулы  .
.
Перепишем формулу  в виде:
в виде:
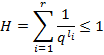
 – длины кодовых слов. Возведем сумму
– длины кодовых слов. Возведем сумму  в степень
в степень  :
:
 ,
,
т.е. возьмем  произведений таких сумм
произведений таких сумм
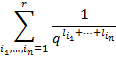
здесь параметры  независимо друг от друга пробегают множество от
независимо друг от друга пробегают множество от  до
до 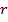 :
:
 ,
,
где  – число представлений числа
– число представлений числа  в виде суммы
в виде суммы  с помощью группировки слагаемых. Т.к. кодирование корректно, то
с помощью группировки слагаемых. Т.к. кодирование корректно, то  .
.
Действительно, 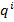 – это общее число слов в кодирующем алфавите длины
– это общее число слов в кодирующем алфавите длины 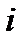 , а каждое решение уравнения
, а каждое решение уравнения 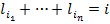 будет соответствовать некоторому кодирующему слову, которых, в силу корректности, не может быть больше чем общее число слов длины
будет соответствовать некоторому кодирующему слову, которых, в силу корректности, не может быть больше чем общее число слов длины  :
:


Достаточность. Пусть числа  удовлетворяют соотношению
удовлетворяют соотношению  . Построим префиксное кодирование типа
. Построим префиксное кодирование типа  .
.
Перепишем сумму  по слагаемым:
по слагаемым:

Наша задача – построение кодовых слов таких, что никакое кодовое слово не начинается на другое кодовое слово. Построим в начале кодовые слова единичной длины, а потом длины 2 и т.д.
Из неравенства  следует, что
следует, что 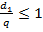 , т.е.
, т.е.  . В кодирующем алфавите есть
. В кодирующем алфавите есть  букв и мы должны выбрать
букв и мы должны выбрать 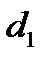 различных кодовых слов единичной длины, а из неравенства
различных кодовых слов единичной длины, а из неравенства  следует, что это действительно можно сделать.
следует, что это действительно можно сделать.
Далее построим кодовые слова длины 2. Тогда выполняется неравенство  , из которого следует, что
, из которого следует, что 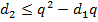 , где
, где  – общее число слов длины 2 в кодовом алфавите, а
– общее число слов длины 2 в кодовом алфавите, а  – число слов длины 2, которые начинаются на кодовые слова единичной длины. Таким образом, число допустимых слов длины 2 равно
– число слов длины 2, которые начинаются на кодовые слова единичной длины. Таким образом, число допустимых слов длины 2 равно 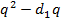 . Из полученного неравенства следует, что мы действительно можем выбрать кодовые слова длины 2, чтобы выполнялись условия префиксности.
. Из полученного неравенства следует, что мы действительно можем выбрать кодовые слова длины 2, чтобы выполнялись условия префиксности.
Допустим, что уже выбраны кодовые слова длины меньшей 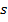 , причем соблюдая условия префиксности. Покажем, что можно выбрать кодовые слова длины
, причем соблюдая условия префиксности. Покажем, что можно выбрать кодовые слова длины 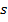 .
.
Из неравенства 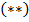 следует, что
следует, что
 ,
,
где 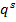 – общее число слов длины
– общее число слов длины 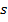 в кодирующем алфавите,
в кодирующем алфавите, 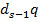 – число слов длины
– число слов длины 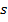 , которые начинаются на кодовые слова длины
, которые начинаются на кодовые слова длины  и т. д.,
и т. д.,  число слов длины
число слов длины 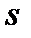 , которые начинаются на кодовые слова длины 1. Таким образом, мы построили префиксное кодирование типа
, которые начинаются на кодовые слова длины 1. Таким образом, мы построили префиксное кодирование типа  .
.
Теория кодирования имеет применение в задачах устойчивой пердачи информации.
Основная литература:
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 285; Нарушение авторских прав?; Мы поможем в написании вашей работы!