
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условные обозначения 1 страница
Формула Грина
Физический смысл криволинейного интеграла II рода
Криволинейный интеграл II рода по координате
Криволинейные интегралы
Криволинейный интеграл II рода по координате записывается в виде

При условии, что  непрерывны в точках дуги MN, а дуга – гладкая кривая
непрерывны в точках дуги MN, а дуга – гладкая кривая  , интеграл существует и вычисляется как определенный интеграл по формуле:
, интеграл существует и вычисляется как определенный интеграл по формуле:
 .
.
Кроме обычных свойств интеграла отметим, что

Если путь интегрирования простая замкнутая кривая L, то его обозначают  , вычисляют в направлении против часовой стрелки и называют циркуляцией.
, вычисляют в направлении против часовой стрелки и называют циркуляцией.
Криволинейный интеграл II рода численно равен работе, которую совершает переменная сила  на криволинейном пути MN.
на криволинейном пути MN.
 Пример. Найти работу силы
Пример. Найти работу силы 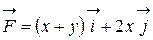 при перемещении по линии
при перемещении по линии 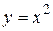 отточки
отточки  к точке
к точке 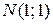 .
.
Решение.


3. Связь между двойными и криволинейными интегралами.
Пусть L граница односвязной области D. 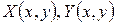 и их частные производные
и их частные производные 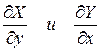 непрерывны в замкнутой области D (включая ее границу L), то имеет место формула:
непрерывны в замкнутой области D (включая ее границу L), то имеет место формула:  .
.
Пример. Вычислить криволинейный интеграл двумя способами: непосредственно и по формуле Грина. L – контур треугольника ABCA 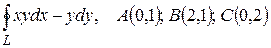 .
.
Решение. 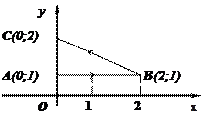 1. Вычислим непосредственно криволинейный интеграл:
1. Вычислим непосредственно криволинейный интеграл:


(BC) – прямая, проходящая через 2 точки, имеет уравнение:

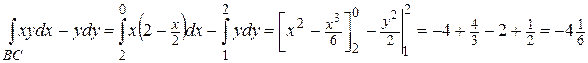 .
.
 .
. 
2. Вычисление интеграла по формуле Грина:


Итак, мы получили тот же результат:
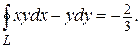
Индивидуальные задания
1 — 10. Найти неопределенные интегралы, в примерах а — б результаты интегрирования проверить дифференцированием.
1. а)  , б)
, б) 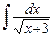 , в)
, в) 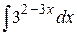 ,
,
г)  , д)
, д) 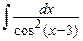 , е)
, е)  .
.
2. а) 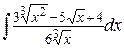 , б)
, б)  , в)
, в)  ,
,
г) 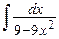 , д)
, д)  , е)
, е)  .
.
3. а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д) 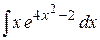 , е)
, е) 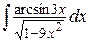 .
.
4. а)  , б)
, б)  , в)
, в) 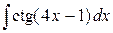 ,
,
г)  , д)
, д)  , е)
, е)  .
.
5. а) 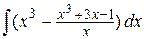 , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
6. а)  , б)
, б) 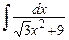 , в)
, в)  ,
,
г)  , д)
, д) 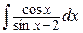 , е)
, е)  .
.
7. а)  , б)
, б)  , в)
, в)  ,
,
г) 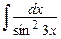 , д)
, д) 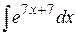 , е)
, е) 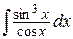 .
.
8. а)  , б)
, б)  , в)
, в) 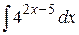 ,
,
г) 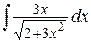 , д)
, д)  , е)
, е) 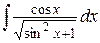 .
.
9. а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
10. а)  , б)
, б)  , в)
, в)  ,
,
г)  , д)
, д)  , е)
, е)  .
.
11 — 20. Найти интегралы, используя метод интегрирования по частям.
11. a) 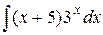 , б)
, б)  .
.
12. а)  , б)
, б)  .
.
13. а)  , б)
, б)  .
.
14. а)  , б)
, б) 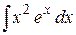 .
.
15. а) 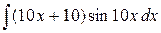 , б)
, б)  .
.
16. а)  , б)
, б)  .
.
17. а)  , б)
, б)  .
.
18. а)  , б)
, б)  .
.
19. а)  , б)
, б) 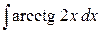 .
.
20. а)  , б)
, б)  .
.
21 — 30. Проинтегрировать рациональные функции.
21. a) 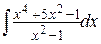 , б)
, б)  .
.
22. а)  , б)
, б)  .
.
23. а) 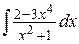 , б)
, б)  .
.
24. а)  , б)
, б) 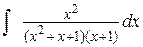 .
.
25. а)  , б)
, б)  .
.
26. а) 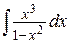 , б)
, б)  .
.
27. а)  , б)
, б)  .
.
28. а)  , б)
, б)  .
.
29. а)  , б)
, б) 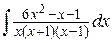 .
.
30. а)  , б)
, б)  .
.
31 — 40. Найти интегралы от тригонометрических функций.
31. а)  , б)
, б)  , в)
, в)  .
.
32. а)  , б)
, б)  , в)
, в) 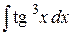 .
.
33. а)  , б)
, б)  , в)
, в)  .
.
34. а)  , б)
, б)  , в)
, в) 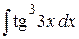 .
.
35. а)  , б)
, б)  , в)
, в) 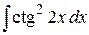 .
.
36. а)  , б)
, б) 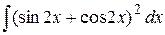 , в)
, в)  .
.
37. а)  , б)
, б) 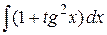 , в)
, в)  .
.
38. а) 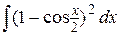 , б)
, б)  , в)
, в) 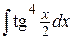 .
.
39. а) 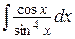 , б)
, б) 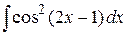 . в)
. в)  .
.
40. а)  , б)
, б)  , в)
, в)  .
.
41 — 50. Найти интегралы с помощью подстановок.
41. а)  , б)
, б)  , в)
, в)  .
.
42. а)  , б)
, б)  , в)
, в)  .
.
43. а)  , б)
, б)  , в)
, в)  .
.
44. а)  , б)
, б)  , в)
, в) 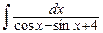 .
.
45. а)  , б)
, б)  , в)
, в)  .
.
46. а)  , б)
, б)  , в)
, в) 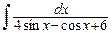 .
.
47. а) 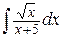 , б)
, б)  , в)
, в)  .
.
48. а)  , б)
, б)  , в)
, в) 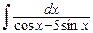 .
.
49. а)  , б)
, б) 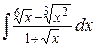 , в)
, в) 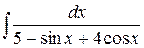 .
.
50. а)  , б)
, б) 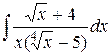 , в)
, в)  .
.
51 — 60. Вычислить определенные интегралы:
51. а)  , б)
, б)  , в)
, в)  .
.
52. а)  , б)
, б)  , в)
, в)  .
.
53. а)  , б)
, б)  , в)
, в)  .
.
54. а)  , б)
, б)  , в)
, в)  .
.
55. а)  , б)
, б)  , в)
, в)  .
.
56. а)  , б)
, б)  , в)
, в)  .
.
57. а)  , б)
, б)  , в)
, в)  .
.
58. а)  , б)
, б)  , в)
, в)  .
.
59. а)  , б)
, б)  , в)
, в)  .
.
60. а)  , б)
, б)  , в)
, в)  .
.
61 — 70. Найти общий интеграл дифференциального уравнения.
61.  . .
| 62.  . .
|
63.  . .
| 64.  . .
|
65.  . .
| 66.  . .
|
67.  . .
| 68.  . .
|
69.  . .
| 70. 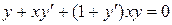 . .
|
71 — 80. Проинтегрировать уравнение.
71.  . .
| 72.  . .
|
73.  . .
| 74.  . .
|
75.  . .
| 76. 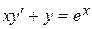 . .
|
77. 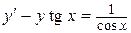 . .
| 78.  . .
|
79.  . .
| 80. 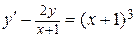 . .
|
81 — 90. Найти частное решение дифференциального уравнения.
| 81. |  , ,
|  , ,
|  . .
|
| 82. |  , ,
|  , ,
|  . .
|
| 83. |  , ,
| 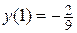 , ,
| 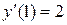 . .
|
| 84. |  , ,
| 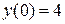 , ,
|  . .
|
 , ,
| 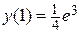 , ,
|  . .
| |
| 86. |  , ,
| 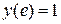 , ,
|  . .
|
| 87. |  , ,
| 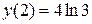 , ,
|  . .
|
| 88. |  , ,
|  , ,
|  . .
|
| 89. |  , ,
|  , ,
|  . .
|
| 90. |  , ,
|  , ,
|  . .
|
91 — 100. Найти частное решение дифференциального уравнения.
|
|
Дата добавления: 2017-01-13; Просмотров: 202; Нарушение авторских прав?; Мы поможем в написании вашей работы!