
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условные обозначения 2 страница
|
|
|
|
| 91. |  , ,
|  , ,
|  . .
|
| 92. |  , ,
|  , ,
| 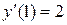 . .
|
| 93. |  , ,
|  , ,
| 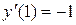 . .
|
| 94. |  , ,
|  , ,
| 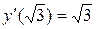 . .
|
| 95. |  , ,
| 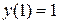 , ,
| 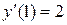 . .
|
| 96. |  , ,
|  , ,
|  . .
|
| 97. |  , ,
|  , ,
|  . .
|
| 98. |  , ,
|  , ,
|  . .
|
| 99. | 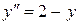 , ,
|  , ,
|  . .
|
| 100. |  , ,
| 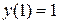 , ,
|  . .
|
101 — 110. Найти общее решение дифференциального уравнения.
101.  .
a) .
a)  , б) , б)  . .
|
102. 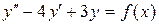 .
a) .
a)  , б) , б) 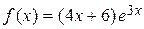 . .
|
103. 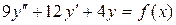 .
a) .
a)  , б) , б)  . .
|
104.  .
a) .
a) 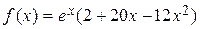 , б) , б) 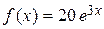 . .
|
105.  .
a) .
a)  , б) , б)  . .
|
106.  .
a) .
a)  , б) , б)  . .
|
107.  .
a) .
a)  , б) , б)  . .
|
108.  .
a) .
a) 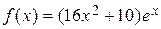 , б) , б) 
|
109.  .
a) .
a)  , б) , б)  . .
|
110. 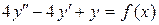 .
a) .
a) 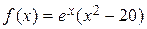 , б) , б)  . .
|
111 — 120. Найти общее решение дифференциального уравнения.
111.  . .
| 112. 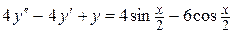 . .
|
113.  . .
| 114.  . .
|
115.  . .
| 116.  . .
|
117.  . .
| 118.  . .
|
119.  . .
| 120.  . .
|
121 — 130. Вычислить двойной интеграл.
121.  .
.
122.  .
.
123.  .
.
124. 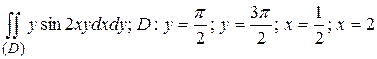 .
.
125.  .
.
126. 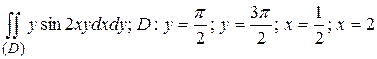 .
.
127.  .
.
128. 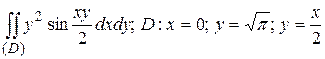 .
.
129.  .
.
130. 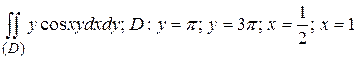 .
.
131 — 140. Найти работу силы  при перемещении вдоль заданной кривой
при перемещении вдоль заданной кривой 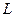 от точки
от точки  к
к 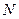 .
.
131. 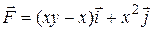 ;
; 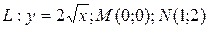 .
.
132.  .
.
133.  ;
;  .
.
134.  ;
;  .
.
135. 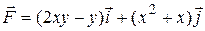 ;
;  .
.
136.  ;
; 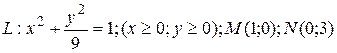 .
.
137. 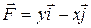 ;
;  .
.
138.  ;
; 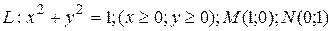 .
.
139. 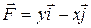 ;
;  .
.
140.  ;
;  .
.
151 — 160. Вычислить интеграл двумя способами: непосредственно и по формуле Грина. 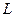 – контур треугольника
– контур треугольника  .
.
151.  ;
; 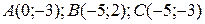 .
.
152.  ;
;  .
.
153.  ;
;  .
.
154.  ;
;  .
.
155.  ;
;  .
.
157.  ;
;  .
.
158.  ;
;  .
.
159.  ;
;  .
.
160.  ;
;  .
.
Литература
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах - ч.I, II – М.: Высшая школа, 1986.
2. Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты) – М.: Высшая школа, 1983.
3. Шипачев В.С. Высшая математика. М.: Высшая школа, 1990.
Методические указания к практическим занятиям по математике
для студентов всех специальностей заочной формы обучения
методические указания
к практическим занятиям
по математике
для студентов всех специальностей
заочной формы обучения
Составители: Кораблева Р.Г., доцент,
Осинцева М.А., ассистент,
Скоробогатова Н.В., ассистент.
Подписано к печати Бум. писч. № 1
Заказ № Уч. изд. л. 1,75 п. л.
Формат 60/90 1/16 Усл. печ. л. 1,75 п. л.
Отпечатано на RISO GR 3750 Тираж экз.
----------------------------------------------------------------------------------------
Издательство «Нефтегазовый университет»
Государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
625000, г. Тюмень, ул. Володарского, 38
Отдел оперативной полиграфии издательства «Нефтегазовый университет»
625000, г. Тюмень, ул. Володарского, 38
G,  – масса (массовый расход или производительность), кг (кг/с) и количество вещества, кмоль;
– масса (массовый расход или производительность), кг (кг/с) и количество вещества, кмоль;
V – объем (объемный расход или производительность), м3 (м3/с)
T, t – температура, К, оС;
Р – абсолютное давление, Па (МПа);
v, r – удельный объем, м3/кг и плотность, кг/м3;
 – универсальная газовая постоянная,
– универсальная газовая постоянная,  = 8314 Дж/(кмоль×К);
= 8314 Дж/(кмоль×К);
m – мольная масса, кг/кмоль;
z – коэффициент сжимаемости;
сp(v)m, сmp(v) – удельные массовые первая и вторая средние изобарная (p) и изохорная (v) теплоемкости, Дж/(кг×К);
f – площадь проходного сечения сопла, м2.
Индексы и символы
o – величины, приведенные к нормальным физическим условиям (н.у.) (Тo = 273,15 К и Ро = 0,1013 МПа);
 – мольные величины;
– мольные величины;
1, 2 – индексы начала и конца процесса;
m – средняя величина;
i – компонент смеси;
кр – критические параметры;
D – разность величин;
', '' – параметры однофазного жидкого и газообразного состояний вещества на линии насыщения.
Основные расчётные соотношения термодинамики
Удельные термодинамическая (ℓ1,2) и потенциальная (w 1,2) работы:
ℓ1,2 =  ; w 1,2 = -
; w 1,2 = -  , Дж/кг. (1)
, Дж/кг. (1)
Характеристическая газовая постоянная:
R =  , Дж/(кг×К). (2)
, Дж/(кг×К). (2)
Уравнение состояния идеального газа:
для 1 кг - закон Клапейрона P×v = R × T, (3)
для любого количества P × V = G × R × T =  × T. (4)
× T. (4)
Уравнения состояния реального газа:
P × v = z × R × T, (5)
где z = f( p, t ), p =  – приведенное давление, t =
– приведенное давление, t =  – приведенная температура;
– приведенная температура;
уравнение Редлиха-Квонга:
 , (6)
, (6)
где коэффициенты  ,
,  ;
;
уравнение Бертло:
 , (7)
, (7)
где коэффициенты  ,
,  ;
;
модифицированное уравнение Бертло:
 . (8)
. (8)
Массовая (mi) и мольная (ri) концентрации смеси:
mi =  ; ri =
; ri =  . (9)
. (9)
Средняя мольная масса смеси:
m m =  =
=  . (10)
. (10)
Удельные массовая (сpm) и молярная ( ) теплоемкости смеси:
) теплоемкости смеси:
cpm =  ;
;  =
=  . (11)
. (11)
Псевдокритические температура (Tпкр) и давление (Рпкр) смеси:
Tпкр =  ; Рпкр =
; Рпкр =  . (12)
. (12)
Первое начало термодинамики по балансу рабочего тела для 1 кг простого тела:
q1,2 = D u1,2 + ℓ1,2 = D h1,2 + w 1,2. (13)
Удельная энтальпия простого тела:
h = u + P × v. (14)
Изменение внутренней энергии и энтальпии 1 кг идеального газа:
D u1,2 = cvm(T2 - T1); D h1,2 = cрm(T2 - T1). (15)
Первое начало термодинамики по балансу рабочего тела для 1 кг идеального газа:
q1,2 = cvm(T2 - T1) + ℓ1,2 = cpm(T2 - T1) + w 1,2 . (16)
Закон Майера:
cpm - cvm = R,  . (17)
. (17)
Показатель адиабаты идеального газа:
k =  =
=  . (18)
. (18)
Изменение удельной энтропии идеального газа:
D s1,2 =  . (19)
. (19)
Уравнение политропы с постоянным показателем:
P × vn = idem; P1 ×  = P2 ×
= P2 ×  . (20)
. (20)
Постоянный показатель политропы:
n =  =
=  =
=  . (21)
. (21)
Характеристика расширения или сжатия:
t 1,2 =  =
=  =
=  , для идеального газа t 1,2 =
, для идеального газа t 1,2 =  . (22)
. (22)
Удельные термодинамическая (ℓ1,2) и потенциальная (w 1,2) работы в политропном процессе:
ℓ1,2 =  ; w 1,2 =
; w 1,2 =  . (23)
. (23)
Удельный термодинамический теплообмен в политропном процессе:
q1,2 =  , (24)
, (24)
для идеального газа показатель изоэнергетического процесса nu = 1.
Удельные термодинамическая (ℓ1,2) и потенциальная (w 1,2) работы в процессах:
- изопотенциальном ℓ1,2 = w 1,2 = P × v ×  = P × v ×
= P × v ×  ; (25)
; (25)
- изобарном ℓ1,2 = P × (v2 – v1); w 1,2 = 0; (26)
- изохорном ℓ1,2 = 0; w 1,2 = v × (P1 – P2). (27)
Теоретическая мощность компрессора:
N к = G ×|w 1,2 |. (28)
КПД термодинамического цикла:
h t =  =
=  =
=  , (29)
, (29)
где ℓц – работа цикла, q1 и q2 –количество подведенной и отведенной теплоты, Tm1 и Tm2 – средние абсолютные температуры рабочего тела в процессах подвода и отвода теплоты.
Теоретическая линейная скорость истечения газов на выходе из сопла:
c2 =  =
=  . (30)
. (30)
Массовый расход газа при истечении через сопло:
G = c ×r f. (31)
Характеристики критического режима истечения:
b кр =  =
=  ; y кр =
; y кр =  . (32)
. (32)
Теоретические линейная (cкр) и массовая (uкр) скорости критического режима истечения:
cкр =  ; uкр = y кр
; uкр = y кр  . (33)
. (33)
Степень сухости пара:
x =  =
=  . (34)
. (34)
Параметры (v, u, h, s) влажного насыщенного пара:
v = (1 - x) × v' + x × v''. (35)
Термический КПД цикла Ренкина с перегретым паром:
 =
=  »
»  , (36)
, (36)
где h1 , h2 –энтальпия водяного пара на входе и выходе из турбины;  –энтальпия конденсата.
–энтальпия конденсата.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 214; Нарушение авторских прав?; Мы поможем в написании вашей работы!