
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тест по теме «Квадратные неравенства»
|
|
|
|
В – 1. В – 2.
1. Сколько решений неравенства содержится среди чисел:
2х2 + 7х – 4 < 0 х2 – 7х – 8 < 0
-3; 0; 1; 2,5. -3; 0; 1; 2,5.
а) ни одного; б) 1; в) 2; г)3.
2. Решите неравенство:
1 – х2 < 0. 9 – х2 > 0.
а) х > 1, в) х < 1, а) х > 3, в) -3 < х < 3,
б) х < -1, г) х < -1; х > 1. б) х < -3, г) х < -3, х > 3.
3. Решите неравенство:
2х2 + 7х – 4 < 0. 3х2 - 4х + 7 ≥ 0.
а) [½; 4], в) (-½; 4), а) [-1; 2⅓], в) (-1; 2⅓),
б) (-4; ½), г) (-∞; -4) U (½; +∞). б) (-∞; +∞), г) (-2⅓; 1].
4. Найдите область определения функции:
у= 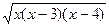 у=
у= 
а) (0; 3) U (4; +∞) в) (-∞; 0) U [3; 4) а) [-5; -2] в) (-∞; -5] U [2; 1) U (1; +∞)
б) [0; 3] U [4; +∞) г) (0;3) б) [1; +∞) г) [-5; -2] U [1; +∞)
Решение рациональных и дробно-рациональных неравенств методом интервалов.
Для решения рациональных дробно-рациональных неравенств обычно применяется метод интервалов:
1. найти корни каждого сомножителя, если неравенство представлено в виде дроби, то отдельно найти корни числителя, корни знаменателя;
2. нанести найденные корни на числовую ось, учитывая строгое или нестрогое неравенство, корни из знаменателя всегда выколотые, четность нечетность количества корней;
3. поставить знак, справа от большего корня, определив знак всего выражения;
4. расставить остальные знаки, при переходе через корень знак неравенства меняется, если корень встречается четное число раз, то при переходе через него знак сохраняется
5. выбрать нужный промежуток, в случае не строгого неравенства к решению неравенства добавить решение уравнения.
Решите неравенства:
1) x2-4x+3<0; 7) (х2-7х+12)(х2-х+2)≤0;
2) х3-3х+2х≤0; 8)  ;
;
3) 2x3+7x-4х<0; 9)  ;
;
4) 3х4-5 х2-2>0; 10) 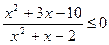 ;
;
5) 4x4-4х2+1≥0; 11)  .
.
6)  12)
12) 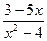
 0.
0.
Перед проведением итогового теста можно предложить учащимся домашнее задание
(х + 4)2(х – 2) < 0, (х – 2)2(х + 1) > 0, 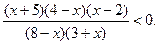

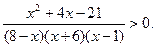
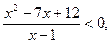
Решение неравенств, содержащих модуль.
Цели и задачи блока:
- повторить решение неравенств, содержащих знак модуля;
- закрепить изученный материал в ходе решения упражнений;
- развитие интеллектуальных способностей, обобщенных умственных умений.
Теоретический материал.
Неравенства, содержащие знак модуля, следующего вида:
 (1)
(1) 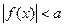 (3)
(3)
 (2)
(2)  (4)
(4)
Решить неравенства можно тремя способами.
Например, рассмотрим решение неравенства 
| 1 способ | 2 способ | 3 способ |
а рассматривается как расстояние на координатной прямой.
Пример:
 , ,
 -расстояние между точками х и 1
Ответ: (-1;3). -расстояние между точками х и 1
Ответ: (-1;3).
| Если а>0, то  и а возводим в квадрат.
Если а<0, то (1) и (2) верны всегда, а (3) и (4) не имеют решений.
Пример: и а возводим в квадрат.
Если а<0, то (1) и (2) верны всегда, а (3) и (4) не имеют решений.
Пример:
 ,
(x-1)2<4,
х2-2x-3<0,
-1<x<3.
Ответ: (-1;3). ,
(x-1)2<4,
х2-2x-3<0,
-1<x<3.
Ответ: (-1;3).
| По определению модуля:
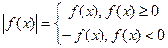 Пример:
Пример:

 или или  1≤х<3.
-1<x<1.
Объединяем оба решения.
Ответ: (-1;3)
1≤х<3.
-1<x<1.
Объединяем оба решения.
Ответ: (-1;3)
|
Опорные неравенства
1)  3)
3) 
2) 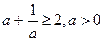 4)
4) 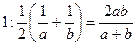
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 632; Нарушение авторских прав?; Мы поможем в написании вашей работы!