
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение методом конечных разностей
|
|
|
|
Исходные данные
| Шифр | Двутавр № | l, м | F, кН | q, кН/м | k0, Н/cм3 |
| 16-1 | 5,2 |
Расчётная схема

Изогнутая ось балки описывается обыкновенным дифференциальным уравнением четвёртого порядка
 . (8)
. (8)
Знак минус в правой части соответствует нагрузке, направленной вниз. Разделим уравнение на 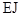 , обозначим
, обозначим
 .
.
и получим вместо (8)
 . (9)
. (9)
 Область непрерывного изменения аргумента
Область непрерывного изменения аргумента  заменим областью дискретного изменения аргумента – сеткой (рис. 3):
заменим областью дискретного изменения аргумента – сеткой (рис. 3):
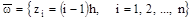 .
.
Множество точек с номерами  называется сеткой, а сами точки – узлами сетки. Вместо функции непрерывного аргумента
называется сеткой, а сами точки – узлами сетки. Вместо функции непрерывного аргумента  будет отыскиваться сеточная функция
будет отыскиваться сеточная функция 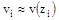 .
.
К уравнению (6) присоединяются граничные условия. На левом конце балки изгибающий момент и поперечная сила в сечении равны приложенным нагрузкам:
 . (10)
. (10)
На правом конце балки – заделка. Поэтому прогиб и угол поворота сечения равны нулю:
 . (11)
. (11)
Пользуясь пятиточечным шаблоном сетки (рис. 4), заменим производные в задаче (6)–(8) конечноразностными соотношениями:
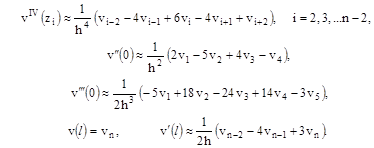 (12)
(12)

Рис. 4
Подстановка (12) в задачу (9)–(11) и несложные преобразования приводят к системе алгебраических уравнений относительно вектора 
 , (13)
, (13)
где
 ,
,
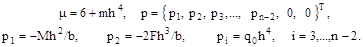
Нулевые элементы матрицы не показаны, значок т в индексе соответствует операции транспонирования.
Система уравнений (13) решается на компьютере с помощью подпрограммы вычислительного комплекса MATLAB, в результате чего становится известным вектор v.
Далее с помощью конечноразностных замен производных вычисляются угол поворота и внутренние силы в сечениях по формулам
 .
.
Реактивный отпор основания определяем с помощью формулы Винклера
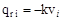 .
.
Результаты счёта, выданные в виде графиков на экран компьютера, изображены на рис. 2.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 220; Нарушение авторских прав?; Мы поможем в написании вашей работы!