Теоретичні питання. 1 страница

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

Решение

S, P, D, F, G, H S, P, D, F, G, H

Решение

а) Возможные оболочки

L= 0, 1, 2, 3, 4 N=2(2L+1) = 2, 6, 10,14,18, 22

Оболочки, заполненные на 1/3 - это P и G. В первом случае S=1, L=1, J=0 и терм ³P₀,

во втором случае спин S=3, поэтому оболочка не подходит к условиям задачи.

б) Подходящая оболочка только D. Для нее 7 электронов дают S=3/2, L=2, J = L+S = 7/2, Поэтому основное состояние будет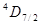

Ответ а) ³P₀ б)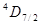

Задача (И.Е.Иродов Задачи по общей физике задача 6.110)

Некоторый атом, кроме заполненных оболочек, имеет три электрона 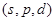и находится в состоянии с максимально возможным для этой конфигурации механическим моментом. Найти в рамках векторной модели атома угол между спиновым и полным механическим моментами данного атома.

Электронные состояния

s: S=1/2, L=0, J=1/2

p: S=1/2, L=1, J=1/2

d: S=1/2, L=2, J=3/2

Максимальный механический момент получается , т.е. складывается из проекций моментов оболочек. Полный спин будет тогда . Квадрат полного спина равен 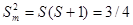, квадрат полного механического момента . Поэтому согласно векторной модели имеем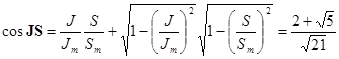

Отсюда искомый угол равен .

Ответ 31^о.

Задача (И.Е.Иродов Задачи по общей физике задача 6.149)

Возбужденный атом имеет электронную конфигурацию и находится при этом в состоянии с максимально возможным механическим моментом. Найти магнитный момент атома в этом состоянии

Максимальный механический момент достигается при сложении проекций спинов и орбитальных моментов электронов незаполненных оболочек, т.е.

При этом .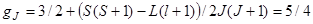

Поэтому

Ответ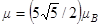

Задача. Вывести зависимость намагниченности от температуры для частицы с полным механическим моментом 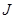в магнитном поле 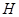. Найти выражение Кюри для парамагнитной восприимчивости при конечной температуре в малом магнитном поле.

Гамильтониан задачи 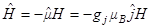имеет энергетические уровни , где целочисленные значения проекции механического момента пробегают значения . Средняя величина намагниченности определяется законом

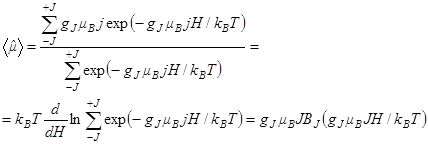
где функция Бриллюэна определяется как

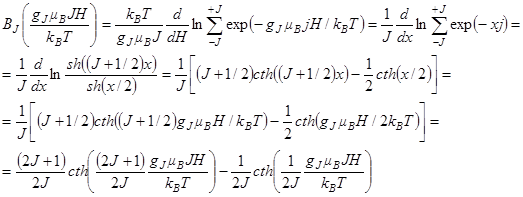
В области высоких температур и малых полей, когда 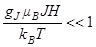имеем

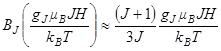, поэтому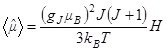

Задача

Получите восприимчивость Паули для модели свободных электронов. Если температура 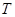мала по сравнению с фермиевской температурой 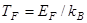, то используя соотношение

,

где - плотность уровней и ее производные по энергии на уровне Ферми , покажите, что зависящая от температуры поправка к восприимчивости Паули для свободных электронов дается выражением

.

Магнитная восприимчивость Паули определяется формулой

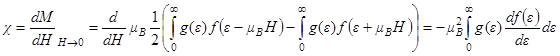
где - распределение Ферми для электронов. В приближении сильного вырождения, когда , можно получить

Для свободных электронов 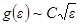. Поэтому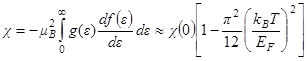

Задача. Оценить значение постоянной 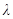и величину молекулярного поля Вейсса для ферромагнетика с температурой Кюри и намагниченностью . Сравнить с параметрами для модели магнитостатического взаимодействия атомов с магнитным моментом атома . Для оценок магнитостатического взаимодействия принять параметр решетк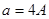и и 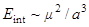, число ближайших соседей .

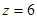Температура Кюри в теории молекулярного поля дается выражением 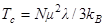. Откуда (, ), .

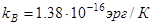Постоянная молекулярного поля связана с энергией межспинового взаимодействия 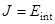следующим образом , где - число ближайших соседей. Поэтому в случае магнитодипольного взаимодействия получим , положив .

Задача

Построить гистерезисную кривую намагничивания монодоменного ферромагнетика при намагничивании под углами 0^о, 45^о и 90^о к оси легкого намагничивания.

Свободная энергия одноосного ферромагнетика с легкой осью вдоль оси записывается в виде

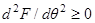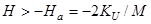1) . Из условия и имеем устойчивые решения в области и 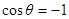в области 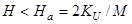и неустойчивое решение в области

2) 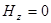устойчивые решения 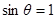в области и 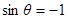в области , а также в области .

3) ,

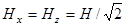, где

Условия равновесия имеют вид

, .

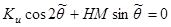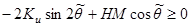Решение дается формулой 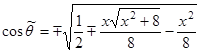, где . Устойчивость решения теряется в точках . Петли гистерезиса имеют вид, представленный на рисунках

Задача

Найти начальную восприимчивость и асимптотику закона намагничивания в сильных магнитных полях при приближения к насыщению для одноосного ферромагнетика с намагниченностью 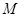и энергией анизотропии при наличии сильной дисперсии осей легкого намагничивания.

Пусть угол между легкой осью и направлением магнитного поля будет 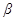, а угол между намагниченностью и полем , когда свободная энергия ферромагнетика будет .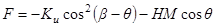

Уравнение для равновесного направления имеет вид

.

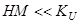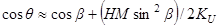В области полей отсюда следует . Поэтому . В результате усреднения по направлениям 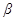, учитывая, что 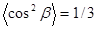, получим начальную магнитную восприимчивость .

В области полей имеем . Поэтому 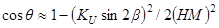. В результате усреднения по направлениям 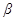получим .

Задача

Оценить плотность энергии анизотропии формы магнитной полоски шириной W = 100 нм и толщиной d = 10 нм с намагниченностью насыщения М =1000 Гс при вращении намагниченности в ее плоскости.

Рассчитаем поле размагничивания в магнитной полоске при поперечном намагничивании. Рассмотрим «магнитостатические заряды на торцах плоски как на рисунке

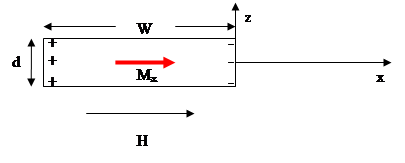
Решение уравнения магнитостатики дается интегралом по торцевым поверхностям. Действительно, если 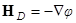, то

.

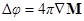Рассмотрим вклад в потенциал от полоски шириной 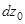на торце. Будем считать, что . Тогд потенциал, создаваемый магнитным зарядом правого торца будет как потенциал от суммы магнитных зарядов узких полосок шириной 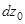, расположенных на высоте на плоскости 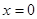, для каждой из которых уравнение имеет вид

,

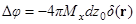где .

Его фундаментальное решение 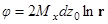дает поле на оси от полоски на высоте

.

Тогда поле размагничивания на оси обусловленное правым торцем будет

.

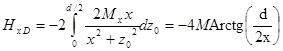Средний по ширине полоски вклад в поле размагничивания равен

где сделано допущение, что . Полный вклад от левого и правого торца даст удвоенную величину , где фактор размагничивания .

Энергия размагничивания будет равна .

Аналогия с электростатикой

Уравнение Пуассона в Гауссовой системе . В вакууме или .

Магнитостатика

или . Поэтому можно ввести магнитный «заряд» . Поверхностный «магнитный» заряд будет равен 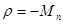. Для элемента поверхности с перпендикулярной компонентой намагниченности в виде линии толщиной dz заряд единицы длины будет 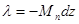. Поле вдоль радиуса от «заряженной» линии будет .

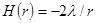Задача

Оценить критический диаметр 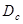возникновения монодоменности магнитного наностолбика при намагниченности насыщения M = 1400 Гс и обменной жесткости .

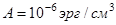Магнитный цилиндр становится монодоменным при радиусе, сравнимом с обменной длиной, а именно когда 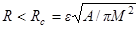, где . Поэтому критический диаметр наностолбика будет равен .

Задача. Оценить критический объем наночастицы с энергией одноосной анизотропии 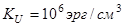и намагниченностью , для которой вероятность спонтанного перемагничивания при комнатной температуре за 5 лет близка к 99%. При расчете принять гиромагнитное отношение , параметр магнитной релаксации Гильберта , .

Вероятность спонтанного перемагничивания за время дается зависимостью 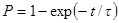, где характерное время термоактивационного переключения магнитной наночастицы дается формулой . Из первого сотношения 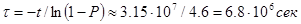. Из второго

Задача.

Определить процент количества перемагниченных наночастиц диаметром D = 20 нм, обладающих намагниченностью М = 800 Гс, постоянной магнитной релаксации и полем анизотропии H_a = 200 Э при комнатной температуре за t = 1 мкс. При расчете принять гиромагнитное отношение .

Вероятность термоактивационного перемагничивания частицы объемом , дается выражением 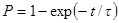, где характерное время термоактивационного переключения магнитной наночастицы . После подстановки и вычислений найдем 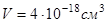, 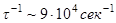. Поэтому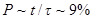

Задача. Сделать оценку минимальной величины вязкого сползания намагниченности за 1 час мелкокристаллической пленки ферромагнетика с намагниченностью насыщения M = 1300 Гс, постоянной магнитной релаксации 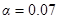и полем анизотропии H_a= 100 Э при комнатной температуре при равномерной дисперсии объема кристаллитов 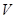в диапазоне от 10³ до 2·10⁴ нм³. При расчете принять гиромагнитное отношение .

Из закона для магнитной вязкости имеем 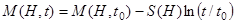, где ,. Полагая, что 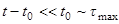, где (, 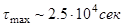), можно получить следующую оценку

.

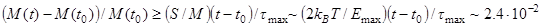Задача

Оценить толщину доменной границы Блоха и обменную длину в ферромагнетике с обменной жесткостью 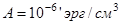, намагниченностью насыщения M = 1400 Гс и полем анизотропии H=100 Э.

Толщина БДГ , обменная длина

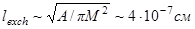
Задача

Найти период доменной структуры с замыкающими магнитными доменами в монокристаллической пленке толщиной h=1 мкм одноосного ферромагнетика с перпендикулярной анизотропией 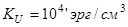. Плотность поверхностной энергии доменных границ считать равной .

Период доменной структуры равен

Задача

Определить количество магнонов в единице объема кубического ферромагнетика с периодом решетки 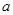, энергией обменного взаимодействия между узлами решетки 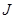, величиной спина в каждом узле решетки , при температурах намного ниже температуры ферромагнитного перехода 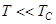. Связать число магнонов с асимптотикой намагниченности при низких температурах.

Указание.

Принять, что энергия магнона – это квант энергии спиновой волны при низкой температуре и дается формулой , где S – спин узла решетки, – волновое число спиновой волны, 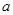– период решетки. Учесть, что сумма квантов спиновых волн (суммарное число магнонов) определяет асимптотику намагниченности при низких температурах в соответствии с формулой .

Количество бозе-частиц с энергией для изотропного кристалла дается формулой

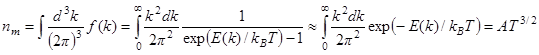где

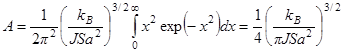, Найденная зависимость определяет закон Блоха 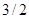для асимптотики намагниченности при низких температурах.

ДЗ2

Задача

Построить полевую зависимость анизотропного магнетосопротивления 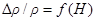пермаллоевой полоски шириной W = 100 нм и толщиной d = 10 нм для магнитного поля, действующего поперек полоски. Максимальная величина эффекта магнетосопротивления в объемном материале 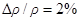. Магнитокристаллической анизотропией пренебречь, учесть только анизотропию формы. Для пермаллоя M = 850 Гс.

Решение.

Фактор размагничивания полоски (см. задачу о полоске ДЗ1) .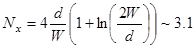

Магнитная энергия полоски в поперечном магнитном поле

,

где - угол между магнитным моментом и направлением тока вдоль полоски.

Из приведенной энергии следует, что 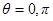при .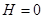

По определению магнетосопротивление находится из формул

,

, где .

Mинимизация энергии по углу дает

Дата добавления: 2017-01-13