Теоретичні питання. 2 страница

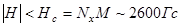при , при .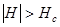

Поэтому имеем

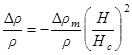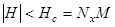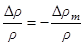при , при .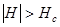

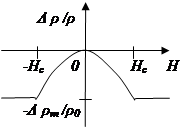
Задача

Построить полевую зависимость магнетосопротивления 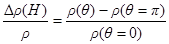, где угол - угол слома намагниченностей магнитных слоев спинового вентиля различной толщины из CoFe с намагниченностью М = 1300 Гс каждый, разделенных прослойкой оксида магния (см. рисунок). Максимальная величина эффекта магнетосопротивления в объемном материале составляет . Толстый слой кобальта толщиной d =20 нм считать полностью закрепленным, а второй свободным. Рассмотреть случай намагничивания полем, действующим в плоскости структуры перпендикулярно оси закрепления намагниченности толстого слоя. Ферромагнитные слои считать имеющими форму диска диаметром D = 100 нм. Магнитостатическое взаимодействие слоев учесть в пренебрежении толщинами промежуточного и незакрепленного слоев по сравнению с толщиной закрепленного слоя. В этом приближении поле магнитостатического поля рассеяния, создаваемое закрепленным слоем в свободном слое, считать приближенно равным полю размагничивания толстого слоя. При расчетах намагничивания структуры пренебречь энергией анизотропии свободного слоя по сравнению с энергией магнитостатического взаимодействия слоев.

Магнетосопротивление определяется формулой , где . В приближении однородного намагничивания свободного слоя энергия структуры для свободного слоя в пренебрежении энергией собственной анизотропии дается выражением

,

где - магнитостатическое поле рассеяния, действующее на свободный слой со стороны закрепленного толстого слоя, - усредненный геометрический фактор, определяющий магнитное поле рассеяния диска с закрепленной намагниченностью в объеме диска свободного слоя. Для тонкого диска можно положить (см лекцию 5). Поэтому .

В отсутствие магнитного поля состояние намагниченности соответствует значению угла 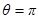, а в насыщенном состоянии . Поэтому относительное изменение магнетосопротивления будет

.

Минимизация энергии по углу слома подрешеток дает 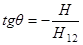, 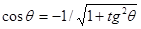. Поэтому

.

Задача

Рассчитать частоту квантового туннелирования ионного кластера из 400 атомов меди в потенциальном рельефе , где , , , , .

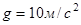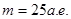
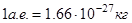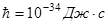Лагранжиан частицы .

Положения равновесия в потенциале 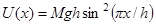будут .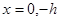

Действие в мнимом времени .

Уравнения движения .

Первый интеграл с учетом граничных условий пр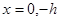и

или .

Инстантонное решение

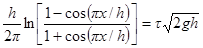
Действие на инстантонной траектории

Откуда 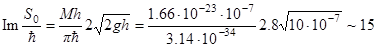. Частота осцилляций вблизи 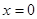следует из уравнения колебаний частицы

.

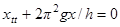
Частота туннелирования (Амплитуда вероятности) равна

,

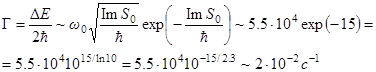Задача

Вывести и оценить экспоненциальный фактор Гамова для частоты туннелирования макроспина в ферромагнитной частице.

Указание: Лагранжиан магнитной частицы записать в следующем виде

,

в котором принять , , 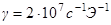, 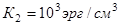при объеме частицы .

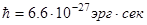
Решение (вывод в лекции 11)

где , , .

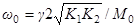Фактор Гамова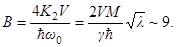

Задача

Рассчитать порог потери устойчивости состояния намагничивания спинового вентиля под действием спин-поляризованного тока в рамках макроспиновой модели для металлической гетероструктуры с перпендикулярной одноосной анизотропией. Намагниченность закрепленного слоя перпендикулярна плоскости слоя.

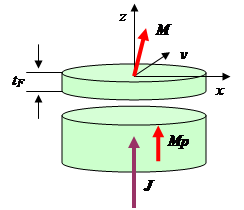
При расчетах принять следующие параметры для свободного слоя: намагниченность , толщина , параметр магнитной релаксации , поле перпендикулярной магнитной анизотропии 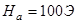, префактор спиновой эффективности передачи вращательного момента Слончевского 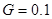. Геометрия намагничивания вертикальная - перпендикулярно слоям вентиля.

Рекомендация:

воспользоваться уравнением ЛЛГ_СБ

,

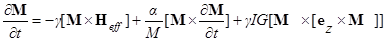где ,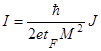

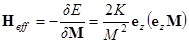
Динамика намагниченности свободного слоя металлического спинового вентиля описывается уравнением Ландау-Лифшица-Гильберта с вращательным членом Слончевского-Берже

,

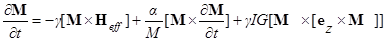где , .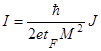

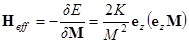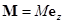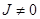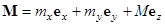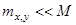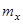В отсутствие тока имеются два положения равновесия . Рассмотрим устойчивость состояния при включении тока . Для этого в линейном приближении положим , где - малые отклонения намагниченности. В результате пренебрежения членами выше линейного, полагая , , где , из уравнения динамики можно получить уравнения для компонент и

Будем искать решение в виде 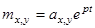, тогда

Из условия разрешимости линейной системы получаем характеристическое уравнение

,

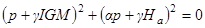которое легко разрешается в комплексных числах

.

Из последнего уравнения следует, что действительная часть показателя 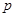становится положительной при токе

.

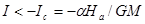Аналогично можно показать, что состояние становится неустойчивым при токах .

Переходя к размерным переменным, получим

Задача

Рассчитать зависимость частоты генерации спиновых колебаний от тока спиновой инжекции в магнитном наностолбике спин-вентильной структуры в вертикальной геометрии намагничивания с легкоплоскостной анизотропией свободного слоя (наведенная анизотропия отсутствует 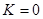) в отсутствие внешнего магнитного поля 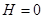. Найти интервал токов возбуждения для свободного слоя со следующими параметрами: намагниченность , толщина , параметр магнитной релаксации , префактор спиновой эффективности передачи вращательного момента Слончевского 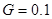. Намагниченность закрепленного слоя перпендикулярна плоскости слоев наностолбика.

Рекомендация:

Воспользоваться уравнением ЛЛГ-СБ в полярных координатах

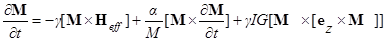
где ,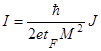

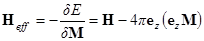
В полярной системе координат

Принять, что в силу аксиальной симметрии во время спиновой прецессии .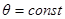

Исходные уравнения динамики Ландау-Лифшица-Гильберта с токовым вращательным членом Слончевского Берже

,

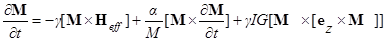где , .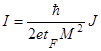

В полярной системе координат

В случае спиновой прецессии в силу аксиальной симметрии стационарное решение находится из условия , . Тогда

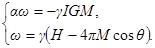
Здесь первое соотношение определяет линейную зависимость частоты от тока (ток может менять знак), а второе дает зависимость амплитуды прецессии (угла ) от частоты, а следовательно и тока. Из последнего соотношения следует, что частота прецессии меняется в пределах

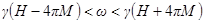
при изменении тока в интервале

.

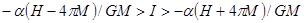Или в размерных переменных

При заданных параметрах задачи в отсутствие магнитного поля 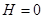прецессия существует в интервале токов

.

При этом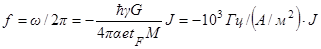

Задача.

Если вероятность спонтанного намагничивания при комнатной температуре за 5 лет в каждой ячейке ЗУ емкостью 1 ТБ (N= бит) должна быть близка к 99%, то каково критическое отношение при указанной вероятности сохранения информации?. Оценить критический объем наночастицы при энергии анизотропии . 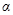=0.02, , 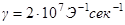. Вероятность сбоя .

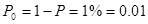Пояснение. Вероятность сохранения информации 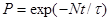, где -время работы, 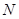- число ячеек, 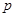- частота переброса между двумя состояниями в магнитной ячейке. Частота теплового переброса в частице объемом 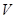дается формулой , где 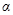- параметр магнитного затухания, 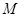- намагниченность, 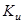- плотность энергии магнитной анизотропии, - гиромагнитное отношение, .

Вероятность сохранения информации за время работы 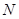ячеек памяти дается формулой 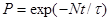. Так как вероятность сбоя мала, т.е. , то . Отсюда имеем условие , где 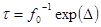, , 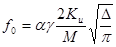. Это дает .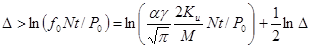

В силу слабой логарифмической зависимости правой части предположим , что оправдывается последующими оценками, будем иметь

.

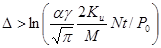Учитывая, что , получаем . В этом случае легко проверить, что предположение выполняется.

Выделенные ниже задачи можно не решать.

Задача

Рассчитать в приближении точечной массы для амплитуду тепловых флуктуаций положения наконечника кремниевого кантилевера АСМ, имеющего размеры 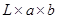=200x30x3 мкм³. Принять для кремния модуль Юнга .

В приближении точечной массы модель кантилевера представляет собой точечный осциллятор с массой 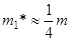и жесткостью 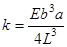. Его энергия . Среднеквадратичная флуктуация положения наконечника находится из условия . Откуда .

Задача

Рассчитать собственную частоту колебаний и эффективную массу точечной модели магнитного наконечника для кремниевого кантилевера АСМ, имеющего размеры 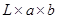=200x30x3 мкм³. Принять для кремния модуль Юнга (), плотность .

Приняв для кремния модуль Юнга (), плотность получим, что для кантилевера размерами 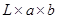собственная частота равна

, где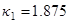

Эффективная точечная масса

,

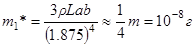где - масса кремниевого кантилевера.

Як змінить сила струму, що протікає крізь провідник, якщо його діаметр збільшити в 2 рази?

Три резистори опором R кожний з’єднані послідовно. Паралельно одному з них підключили резистор опором R/2. Як зміниться еквівалентний опір всього кола?

Є три резистори опорами: R₁ = 50 Ом; R₂ = 25 Ом і R₃ = 100 Ом. Як їх необхідно з’єднати, щоб еквівалентний опір дорівнював 70 Ом.

Для схеми, наведеної на рисунку визначити еквівалентний опір кола, якщо

1. S₁ і S₂ розімкнені.

2. S₁ розімкнений, а S₂ замкнений.

3. S₁ і S₂ замкнені.

Маємо 8 резисторів опором 10 Ом. Як їх можна зєднати, щоб загальний опір склав 20 Ом.

Задача 1

В електричному колі з джерелом E = const, напруги U₁ = U₂; I₁ = 3 A; I₃₄ = 2,5 A; I₄ = 1,5 A. Знайти струми в усіх гілках при збільшенні R₄ у 3 рази.

Задача 2

При напрузі 60 В в колі проходить струм 2,5 А. Який додатковий опір необхідно включити, щоб в колі проходив струм 2 А:?

Задача 3

Який опір необхідно включити паралельно резистору опором 100 Ом, щоб їх загальний опір склав 20 Ом?

Задача 4

Напругу 24 В подано на два резистори, з’єднані послідовно, внаслідок чого крізь них протікає струм 0,6 А. Якщо резистори з’єднані паралельно, сумарна сила струму дорівнює 3,2 А. Знайти опір резисторів.

Задача 5

Визначити довжину мідного провідника, намотаного на котушку, якщо при подачі на виводи цієї котушки напруги 27 В, значення струму склало 5 А. Діаметр провідника 0,8 мм. Питома електрична провідність міді ρ = 0,017 .

Задача 6

Маємо куб з токої проволоки. Опір кожного ребра кубіка R. Знайти еквівалентний опір між точками А і В.

Дата добавления: 2017-01-13