Расчетные усилия

Нагрузки

Геометрические размеры оси арки

При расчетном пролете l = 60 м и стреле подъема ее f = 11 м радиус арки находим по формуле

r = (l ² + 4 f ²)/(8 f) = (60² + 4×11²)/(8×11) = 46,41 м;

центральный угол дуги полуарки α определяем из выражения

cos α = (r - f)/ r = (46,41 - 11)/46,41 = 0,763,

откуда α = 40°16 '. Центральный угол дуги арки 2α = 80°32 ', длина дуги арки

S = (π r ×2α)/180° = (3,14×46,41×80,54°)/180° = 65,2 м.

Координаты точек оси арки y для вычисления моментов M находятся по формуле

,

где Д = r - f = 46,41 - 11 = 35,41 м и приведены в табл. 26.

Таблица 26

Координаты	Значение координат точек оси арки, м
x
y		3,69	4,9	6,47	8,51	9,91	10,73
φ	40°15 '	32°36 '	26°51 '	25°30 '	18°51 '	12°27 '	6°12 '

Постоянные расчетные нагрузки на 1 м² горизонтальной проекции покрытия определяются с введением коэффициента перегрузки n в соответствии со СНиП II-6-74, пп. 2.2. Нормативные нагрузки умножаются на коэффициент k = S / l = 64,4/60 = 1,07, учитывающий разницу между длиной дуги арки и ее проекцией.

Вес снегового покрова для III района P ₀ = 1 кН/м² горизонтальной проекции; коэффициент c ₁, учитывающий форму покрытия, в соответствии со СНиП II-6-74, табл. 5, п. 5.5 будет равен:

c ₁ = l /(8 f) = 60/(8×11) = 0,682;

тогда нормативная равномерно распределенная снеговая нагрузка

P ^н_сн = P ₀× c ₁ = 1×0,682 = 0,682 кН/м².

Собственный вес арки в зависимости от нормативного веса кровли и снега определим по формуле прил. 2

g ^н_св = (g ^н_п + P ^н_св)/[1000/(K _св l) - 1] = (0,594 + 0,682)/[1000/(4×60) - 1] = 1,276/3,16 = 0,404 кН/м².

Сбор постоянных нагрузок арочного покрытия приведен в табл. 27. Полная нормативная нагрузка от собственного веса g ^н = 0,998 кН/м² горизонтальной проекции.

Отношение нормативного собственного веса покрытия к весу снегового покрова g ^н/ P ₀ = 0,998/1 = 0,998; коэффициент перегрузки n = 1,41 (СНиП II-6-74), тогда расчетная снеговая нагрузка на 1 м² горизонтальной проекции покрытия

P ₁ = P ₀ nc ₁ = 1×1,41×0,682 = 0,962 кН/м².

Таблица 27

Наименование элемента	Нормативная нагрузка, кН/м^2	n	Расчетная нагрузка, кН/м^2
Плита покрытия
асбестоцементный лист	0,187	1,1	0,206
каркас и утеплитель	0,364	1,2	0,437
Кровля из оцинкованной стали	0,043	1,1	0,047
Арка	0,404	1,1	0,444
Подвесное оборудование	-	-	0,03
Итого	0,998	-	1,164

При снеговой нагрузке, распределенной по треугольнику, коэффициент c ₂ = (2 + 2,2)/2 = 2,1 по интерполяции и

P ₂ = P ₀ nc ₂ = 1×1,41×2,1 = 2,90 кН/м².

Расчетные нагрузки, приходящиеся на 1 м горизонтальной проекции арки при шаге арок 6 м, находятся:

от собственного веса покрытия по табл. 27

q _р = 1,164×6 = 7 кН/м;

от снега

P _1р = 0,962×6 = 5,8 кН/м;

P _2р = 2,96×6 = 17,8 кН/м.

Статический расчет арки

Схемы нагрузок показаны на рис. 43.

Расчет арки производим для следующих сочетаний нагрузок 1) постоянной и снеговой, равномерно распределенной по всему пролету; 2) постоянной по всему пролету и снеговой, равномерно распределенной на половине пролета, 3) постоянной по всему пролету и снеговой, распределенной по треугольнику на половине пролета (СНиП II-6-74, п. 5.3)

Определяем усилия в арке при разных схемах нагружения от нагрузки 10 кН/м:

Рис. 43. Схема нагрузок от собственного веса и снега, действующих на арку

а) от равномерно распределенной нагрузки по всему пролету:

вертикальные опорные реакции

V_А = V_В = l /2 = 60/2 = 300 кН;

горизонтальный распор

H = l ²/(8 f) = 60²/(8×11) = 410 кН;

б) от равномерно распределенной нагрузки на полупролете (слева):

вертикальные опорные реакции:

V_А = 3 l /8 = 3×60/8 = 225 кН;

V_В = l /8 = 60/8 = 75 кН;

горизонтальный распор

H = l ²/(16 f) = 60²/(16×11) = 205 кН;

в) от распределенной по треугольнику нагрузки наполовине пролета (слева):

вертикальные опорные реакции

V_А = 5 l /24 = 5×60/24 = 125 кН;

V_В = l /24 = 60/24 = 25 кН;

горизонтальный распор

H = l ²/(48 f) = 60²/(48×11) = 68,2 кН.

Значения M_x, Q_x и N_x для загружения (п. а) и на участке 0 ≤ x ≤ l /2 (п. б) вычислены по формулам:

M_x = V_А × x - x ²/2 - H × y;

Q_x = - H sin φ + (V_А - x)cos φ;

N_x = H cos φ + (V_А - x)sin φ.

На участке l /2 ≤ x ≤ l - по формулам:

M_x = V_В (l - x) - Hy;

Q_x = H sin φ - V_В cos φ;

N_x = - H cos φ - V_В sin φ.

Для загружения (по п. в) вычисления проводились по формулам

на участке 0 ≤ x ≤ l /2:

M_x = V_А [ x - 3,2(l - x) x ²/ l ²] - Hy;

Q_x = V_А [1 - 4,8(l - x) x ²/ l ²]cos φ - H sin φ;

N_x = H cos φ + V_А [1 - 4,8(l - x) x ²/ l ²]sin φ;

на участке l /2 ≤ x ≤ l:

M_x = V_В (l - x) - Hy;

Q_x = H sin φ - V_В cos φ;

N_x = - H cos φ - V_В sin φ.

На рис. 44 даны эпюры изгибающих моментов от нагрузок по пп. а, б, в и от сочетания нагрузок по схемам 1, 2 и 3. На рис. 45 даны эпюры нормальных и поперечных сил от сочетания нагрузок по схемам 1, 2 и 3. Вертикальные опорные реакции V_А и V_В и распор H для различных схем загружения соответственно равны 384, 384, 523 кН (схема 1); 341, 254, 406 кН (схема 2) и 433, 255, 408 кН (схема 3).

Как видно из эпюр, расчетной является схема загружения 3 как по положительным, так и по отрицательным моментам. Максимальный положительный момент имеется в сечениях с абсциссой x = 10 м, а отрицательный - с абсциссой x = 50 м.

M ₁₀ = 343 кН×м; N ₁₀ = -461 кН; M ₅₀ = -477 кН×м; M ₅₀ = -449 кН.

Предварительное определение поперечных размеров сечения арок

Рис. 44. Эпюры изгибающих моментов в арке от расчетных нагрузок и от их сочетания

а) постоянной (собственный вес арки); б) снеговой, равномерно распределенной по всему пролету; в) снеговой, равномерно распределенной на половине пролета; г) снеговой, распределенной по треугольнику на половине пролета; 1 - постоянной (а) и снеговой (б); 2 - постоянной (а) и снеговой (в); 3 - постоянной (а) и снеговой (г)

Рис. 45. Эпюры нормальных (N) и поперечных (Q) сил в арке от сочетания расчетных нагрузок

1 - постоянной (а) и снеговой (б); 2 - постоянной (а) и снеговой (в); 3 - постоянной (а) и снеговой (г)

Подбор сечения арки

Предварительное определение размеров поперечного сечения арок производим по СНиП II-25-80, п. 4.17, формула (28):

N / F _расч + M _д/ W _расч ≤ R _с.

Приняв h / b = β, получим

h ³ - β Nh / R _с - 6β M /(ξ R _с) = 0. (47)

Уравнение (47) приводим к виду

h ³ + 3 ph + 2 q = 0, (48)

где p = -β N /(3 R _с);

q = -3β M /(ξ R _с);

β = 5 ¸ 6;

ξ = 0,5 ¸ 0,8;

R _с - расчетное сопротивление древесины сжатию с учетом коэффициентов условий работы по пп. 3.1 и 3.2 и коэффициентов надежности по назначению конструкций согласно стандарту СТ СЭВ 384-76.

Поскольку q >> p, дискриминант уравнения (48) Д = q ² + p ² > 0 и оно имеет одно действительное и два мнимых решения. Согласно формуле Кардано, действительное решение h = U + V,

где ;

Подбор сечения арки

Учитывая уникальный характер здания по степени ответственности, для изготовления арок принимаем пиломатериал из древесины сосны 1-го сорта толщиной 4,2 см. Коэффициент надежности по назначению γ _n = 1.

Оптимальная высота поперечного сечения арки находится в пределах (1/40 - 1/50) l = = (1/40 - 1/50)6000 = 150 - 120 см.

Согласно пп. 3.1 и 3.2, при h > 120 см, δ_сл = 4,2 см и r_k / a = 4641/4,2 = 1105 > 500 коэффициенты условий работы будут m _б = 0,8, m _сл = 0,95, m _гн = 1; соответственно расчетное сопротивление сжатию и изгибу

R _с = R _и = 0,8×0,95×1,0×16/1,0 = 12,2 МПа.

Для определения поперечных размеров сечения арки пользуемся уравнением (47). Принимаем β = h / b = 5,5; ξ = 0,65 и определяем высоту и ширину сечения арки h = 1285 мм и b = 1285/5,5 = 234 мм ≈ 240 мм.

Принимаем поперечное сечение арки b ´ h = 240 ´ 1344 мм из 32 слоев толщиной 42 мм.

Расчет арки на прочность выполняем в соответствии с указаниями СНиП II-25-80, п. 4.17, формула (28).

Определяем гибкость согласно СНиП II-25-80, пп. 4.4 и 6.25, формула (9):

λ = l ₀/ r = 0,58 S / = 0,58 S / = 0,58 S /(0,29 h) = 0,58×65,2/(0,29×1,344) = 97.

Согласно п. 6.27, при определении коэффициента ξ вместо N в формулу (30), п. 4.17, СНиП II-25-80 надо поставить N ₃₀ = 408 кН - сжимающее усилие в ключевом сечении для расчетного сочетания нагрузок (см. рис. 45):

ξ = 1 - λ² N ₃₀/(AR _с F _бр) = 1 - 97²×408×10³/(3000×12,2×240×1344) = 0,675;

момент

M _д = M /ξ = 447/0,675 = 662 кН×м;

расчетный момент сопротивления

W _расч = 6 h ²/6 = 240×1344²/6 = 72,253×10⁶ мм³.

Подставив эти значения в формулу (28) СНиП II-25-80, получим:

N / F _расч + M _д/ W _расч = 449000/322600 + 662×10⁶/72,253×10⁶ = 1,4 + 9,2 = 10,6 < 12,12 МПа,

т.е. прочность сечения достаточна.

Проверим сечение на устойчивость плоской формы деформирования по формуле (33) п. 4.18 СНиП II-25-80.

Покрытие из плит шириной 150 см раскрепляет верхнюю кромку арки по всей длине, откуда

l _р = 2×150 см < 140× b ²/(hm _б) = 140×24²/(134,4×0,8) = 750 см,

т.е. имеет место сплошное раскрепление при положительном моменте сжатой кромки, а при отрицательном - растянутой, следовательно, показатель степени n = 1 в формуле (33), СНиП II-25-80.

Предварительно определяем:

а) коэффициент φ_М по формуле (23), п. 4.14, СНиП II-25-80 с введением в знаменатель коэффициента m _б согласно п. 4.25 настоящего Пособия:

φ_М = 140 b ² K _ф/(l _р hm _б) = 140×24²×1,13/(3260×131,4×0,8) = 0,26.

Согласно СНиП II-25-80, п. 4.14, к коэффициенту φ_М вводим коэффициенты K _жм и K _нм. С учетом подкрепления внешней кромки при m > 4 K _жм = 1

K _нм = 0,142 l _р/ h + 1,76 h / l _р + 1,4α_р = 142×3260/134,4 + 1,76×134,4/3260 + 1,4×0,702 = 4,5;

φ_м K _нм = 0,26×4,5 = 1,17;

б) коэффициент φ по СНиП II-25-80, п. 4.3, формула (8) для гибкости из плоскости

φ = A /λ² _y = 3000[(0,5 S /(0,29 b)²] = 3000×0,29²×24²/(0,5×6520²) = 0,014.

Согласно СНиП II-25-80, п. 4.18, к коэффициенту φ вводим коэффициент K _{н N}, который при m > 4 равен:

K _{н N} = 0,75 + 0,06(l _р/ h)² + 0,6α_р l _р/ h = 0,75 + 0,06(3260/134,4)² + 0,6×0,702×3260/134,1 = 46,27;

φ K _{н N} = 0,014×46,27 = 0,6648.

Подставив найденные значения в формулу (33) СНиП II-25-80, получим

N /(F _брφ R _с) + M _д/(W _брφ_м R _и) = 449×10³/(322×10³×0,6448×12,2) + 662×10⁶/(72,253×10⁶×1,17×12,2) = 0,18 + 0,65 = 0,83 < 1.

Таким образом, условие устойчивости выполнено и раскрепления внутренней кромки в промежутке между пятой и коньковым шарниром не требуется.

Расчет узлов арки

Опорный узел (рис. 46)

Расчетная нормальная сила N = 649 кН, поперечная сила Q = 66 кН (см. рис. 45).

Материалы шарнирного соединения в пяте и коньке, сталь марки ВСт3кп2 по ГОСТ 380-71 с изм. и гнутый профиль из трубы диаметром 50 мм с толщиной стенки 5 мм по ГОСТ 8732-78 с изм.

Проверка напряжений в шарнире на смятие производится по формуле (64), п. 5.38, СНиП II-23-81

F /(1,25 rl) ≤ R_{l р}γ_с;

требуемый радиус шарнира

r = F /(1,25 lR_{l р} v _с) = 649×10³(1,25×160×168×1) = 19,4 мм.

Рис. 46. Опорный узел арки

1 - стальной шарнир; 2 - боковые ребра опорного башмака; 3 - оголовок; 4 - гнутый профиль; 5 - среднее ребро башмака; 6 - болты; 7 - опорная плита; 8 - накладки; 9 - фундамент

Конструктивно принимаем стержень d = 40 мм. При этом для гнутого профиля башмака принимаем половину трубы d = 50 мм с толщиной стенки 5 мм.

Производим проверку торцевого упора арки на смятие. Расчетное сопротивление смятию R _см = R _с = R _и = 12,2 МПа;

требуемая площадь смятия

F _см = N / R _см = 649×10³/12,2 = 5,32×10⁴ мм²,

откуда при b = 210 мм

l ≥ F _см/ b = 5,32×10⁴/240 = 222 мм, принимаем l = 400 мм.

Исходя из этих размеров, назначаем ширину и длину башмака соответственно 200 и 400 мм. Усилие от шарнира передается на башмак через сварной профиль из пластин, имеющий два боковых и одно среднее ребра (см. рис. 46). Тогда площадь смятия торца арки под башмаком

F _см = 200×400 = 8×10⁴ мм;

напряжения смятия

σ_см = 649×10³/8×10⁴ = 8,1 < 12,2 МПа;

площадь смятия ребер под сварным профилем

F _см = (2×4 + 12)δ = 20δ;

требуемая толщина ребер башмака

δ = N /(20 R_{l р} v _с) = 649×10³/(20×168×1) = 19,3 мм.

Принимаем ребра толщиной 20 мм. В пределах башмака оголовок работает как плита, защемленная с трех сторон и свободная короткой стороной, с размером в плане 200 ´ 160 мм. Максимальный изгибающий момент определяем по формуле (см. Рохлин И.А., Лукашенко И.А., Айзен А.М. Справочник конструктора-строителя. Киев, 1963, с. 192) M = 0,085 ql ² = 0,085×8,1×160² = 1,76×10⁴ Н×мм.

Требуемый момент сопротивления

W = δ²/6 = M / R _и = 1,76×10⁴/220 = 80 мм³,

откуда

δ = 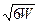= = 21,9 мм.

Принимаем лист толщиной 22 мм.

Концевые части пластины оголовка подвергаются изгибу как консольные от равномерно распределенной нагрузки интенсивностью, соответствующей напряжениям смятия по всей внутренней площадке оголовка от нормальной силы

q = Nb _пл/ F _см = 649×10³×200/(750×200) = 865 Н/мм.

Безопасное расстояние x от края пластины оголовка до ребер башмака определяем из равенства:

W = M _конс/(1,2 R _и) = 200×22²/6 = 865 x ²/(1,2×2 R _и),

откуда x = = 99 мм.

Таким образом, конструктивно длину башмака принимаем

a = 750 - 2×99 = 552 ≈ 600 мм.

На болты, присоединяющие оголовок, действуют усилия, вызываемые поперечной силой при третьей схеме загружения:

N _б = Q (15 + 2,2 + 17,8/3)/75 = 66×23/75 = 20,24 кН.

Необходимый диаметр болта определим, исходя из его несущей способности по изгибу согласно СНиП II-25-80, п. 5.16:

T _б = n 2,5 d ² = N _б, при n = 2;

d = = = 2,01 см.

Принимаем болты диаметром 20 мм.

Коньковый шарнир (рис. 47)

Расчет опорной пластины

Принимаем пластину размером 300 ´ 200 мм. Нормальная сила, сжимающая пластину N = 52,5 кН. Напряжения смятия торца арки в ключе

σ_см = N / F _см = 525×10³/(300×200) = 8,8 < 12,2 МПа.

Рис. 47. Коньковый узел арки

1 - упорный штырь; 2 - опорная пластина; 3 - спаренный штырь; 4 - оголовок; 5 - болты; 6 - накладка

Толщину пластины находим из условия ее работы на изгиб по схеме двухконсольной балки, для которой нагрузка

q = 52,5/0,3 = 1750 кН/м;

изгибающий момент

M = 1750×0,135²/2 = 16 кН×м.

Требуемый момент сопротивления (с учетом пластичности)

W = M /(R _и×1,2) = 16×10⁶/(220×1,2) = 60,6×10³ мм³.

Требуемая толщина пластины

δ = = = 43 мм.

Принимаем толщину пластины 45 мм.

Расчет упорного штыря производим на изгиб как консоли. Изгибающий момент

M = Q ×50 = 44×10³×50 = 220×10⁴ Н×мм;

требуемый момент сопротивления с учетом пластичности

W = 220×10⁴/(220×1,2) = 8,3×10³ мм³;

при ширине штыря b = 100 мм требуемая толщина

δ = = 22,3 мм.

Принимаем δ = 30 мм.

Аналогично рассчитываются спаренные штыри, вваренные справа в опорную пластину. Оголовок и его крепление принимаем таким же, как и в опорных узлах арки.

Безопасное расстояние от края пластины оголовка до опорной пластины определяем так же, как при расчете пятового шарнира,

где

q = 525×10³/750 = 700 Н/мм,

тогда длину опорной пластины конструктивно принимаем 750 - 2×110 = 530 ≈ 540 мм.

Пример 2. Запроектировать трехшарнирную стрельчатую арку для неотапливаемого склада сыпучих материалов.

Исходные данные

Арки постоянного сечения, пролет l = 24 м, стрела подъема f = 6 м > l /6 при шаге 4,5 м, опоры железобетонные (рис. 48). Район строительства III по снеговой нагрузке и I по скоростному напору ветра.

Ограждающая часть покрытия состоит из прогонов с шагом 1,5 м, укладываемых непосредственно на арки. По прогонам устраивается кровля из асбестоцементных листов УВ-1750.

Устойчивость арок из плоскости обеспечивается прогонами и деревянными диагональными элементами, которые расположены в торцах здания и через 22,5 м вдоль здания, образуя поперечные связевые фермы. Прогоны прикреплены к верхним граням арок, а в коньке и пятах полуарок поставлены продольные элементы с упором в боковые грани арок.

Дата добавления: 2017-01-14