Уравнение Бернулли

Уравнение Клапейрона-Менделеева.

Состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением , объемом 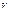и температурой . Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением

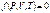, (6.13) где каждая из переменных является функцией двух других.

Уравнение Клапейрона: 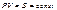,(6.14) в котором — газовая постоянная, различная для разных газов.

Уравнение Клапейрона - Менделеева записывается в виде: , (6.15) =8,31 Дж/(моль×К).

Это уравнение состояния идеального газа.

Выделим в стационарно текущей жидкости объем трубки тока, ограниченный сечениями . Пусть в месте сечения , скорость жидкости равна , давление , а высота, на которой расположено сечение . Параметры в месте сечения : . За время 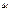сечения переместятся, перемещение является бесконечно малым, поэтому сечение практически остается таким же (рис.3.3). Согласно закону сохранения энергии: изменение полной энергии несжимаемой жидкости в объеме между сечениями равно работе неконсервативных сил по перемещению жидкости, изменению потенциальной энергии.

Рис. 3.3

Полная энергия жидкости массой в месте сечения равна работе : .(3.5)

C другой стороны, работа , затрачиваемая при перемещении объема жидкости между сечениями за промежуток времени на расстоянии определяется ,(3.6)

, . Полная энергия жидкости состоит из суммы кинетической и потенциальной энергий жидкости массой : (3.7) (3.8)

Подставляя выражения (3.7), (3.8), в (3.5) и приравнивая (3.5) и (3.6), получаем (3.9)

Согласно уравнению неразрывности изменение объема

.Разделив выражение (3.9) на получаем: ,

- плотность жидкости.

Так как сечения выбирались произвольно, можно записать 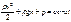, (3.10)

- статическое давление, - динамическое давление,

- гидростатическое давление, связанное с высотой. Выражение (3.10) – это уравнение Бернулли.

Оно представляет собой закон сохранения энергии применительно к установившемуся течению идеальной жидкости.Для горизонтальной трубки тока () выражение (3.10) принимает вид: . (3.11)

Выражение (3.11) представляет собой полное давление.

Уравнение Бернулли устанавливает важную взаимосвязь между . Это позволяет в любой момент времени определить, например, скорость течения жидкости при неизменной .

Дата добавления: 2017-01-14