Гармонические колебания и их характеристики

Начало термодинамики.

Применительно к термодинамическим процессам закон сохранения и превращения энергии в результате обобщения опытных данных формулируется в виде Первого начала термодинамики: теплота dQ, сообщаемая системе, расходуется на изменение её внутренней энергии dU и на совершение ею работы против внешних сил dA: (7.16). Из выражения (7.16) в системе СИ следует, что количество теплоты выражается в джоулях, Дж.

Вводится понятие теплоёмкости.

Удельная теплоёмкость вещества – величина равная количеству теплоты, необходимому для нагревания 1кг вещества на 1^оК: (7.17). Единица удельной теплоёмкости - джоуль, на килограмм кельвин, (Дж/ (кг×К)).

Молярная теплоёмкость – величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1^оК: 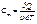,(7.18); – количество вещества.

Единица молярной теплоёмкости – джоуль на моль-кельвин, (Дж/(моль×К)).

Колебаниями называются движения или процессы, которые характеризуются определённой повторяемостью во времени.

Различают механические, электромагнитные колебания и т.д.

Колебания называются свободными, если они совершаются за счёт первоначально сообщённой энергии.

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется во времени по закону синуса (косинуса).

Гармонические колебания описываются уравнением вида:

.(4.1); – амплитуда колебаний, - круговая (циклическая) частота, - начальная фаза колебаний в момент времени , – фаза.

Графически гармонические колебания изображаются методом векторных диаграмм (рис.4.1).

Рис. 4.1. Из произвольной точки O, выбранной на оси под углом , равным начальной фазе колебаний, откладывается вектор , модуль которого равен амплитуде рассматриваемого колебания. Если вектор привести во вращение с угловой скоростью , равной циклической частоте колебаний, то проекция вектора будет перемещаться по оси и изменять значения от -A до +A, а колеблющаяся величина будет изменяться по з-ну: s=Acos(w₀t+φ)

Определённые состояния системы, совершающей гармонические колебания, повторяются через промежуток времени T, называемый периодом колебания. За период колебаний фаза получает при-ращение 2π, т.е. w₀(t+T)+φ=(w₀t+φ)+2π (4.2), Откуда: T=2π/w₀ (4.3)

Величина, обратная периоду колебаний, называется частотой колебаний: v=1/T (4.4)

Сравнивая выражения (4.3) и (4.4), получаем: w₀=2πv (4.5)

Единицей частоты является герц, (Гц). 1Гц – частота периодического процесса, при которой за 1с совершается 1 цикл процесса.

1-ая и 2-ая производная от гармонически колеблющейся величины s: ds/dt=Aw₀sin(w₀t+φ)=Aw₀cos(w₀t+φ+π/2) (4.6)

d²s/ dt²=-Aw₀²cos(w₀t+φ)=Aw₀²cos(w₀t+φ+π) (4.7)

Амплитуды колебаний в выражениях (4.6) и (4.7) равны Aw₀ и Aw₀²; фаза колебания в выражении (4.6) отличается от фазы колебания в выражении (4.7) на π/2, а фаза колебания в выражении (4.7) от фазы в выражении (4.1) - на π.Из уравнения (4.7) и (4.1) следует, что дифференциальное уравнение гармонических колебаний

d²s/ dt²+ w₀²s=0 (4.8)

гдеs= Acos(w₀t+φ) является решением этого уравнения.

13. Вынужденные колебания. Резонанс. Чтобы в реальной системе получить незатухающие коле-бания, надо компенсировать потери энергии с помощью пе-риодически действующей силы. В случае механических ко-лебаний и вынуждающей силы F=F₀ cos wt для пружинного маятника массой m можем записать закон движения: m(d²s/dt²)=-ks-rs+F₀coswt (4.25), где:F = -kx – упругая сила, F=-rv=-rx-сила трения,r–коэффициент сопротивления, w₀= -циклическая частота и , выраж.4.25 превращается в (4.26) Колебания, изменяющиеся под действием внешней периодически изменяющейся силы, называются вынужденными механическими колебаниями. В установившемся режиме колебания происходят с частотой w и являются гармоническими, амплитуда и фаза колебаний определяется выражениями где , (4.27); (4.28) также зависит от w. Рассмотрим зависим. амплитуды вынужденных колебаний A от частоты w. При max значении амплитуды смещения A (выражение (4.28)) частота w на-зывается резонансной частотой и определяется w_р = (4.29). Явл-е резкого ↑ амплитуды вынужден-ных колебаний при приближении частоты вынуждающей силы к частоте, равной или близкой к собственной частоте колебательной системы, называются резонансом (рис. 4.8). Подставив выражение (4.30) в (4.28) получаем значение ам-плитуды при резонансе A_p= (4.30) Явление резонан-са может быть как вред-ным, так и полезным. В биологии действие излучений мож быть полезно, напр, при лечении микроволновым излучением (резонансная терапия) и т.д.

Дата добавления: 2017-01-14