КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вариньон теоремасы. 3 страница
55. Нүктенің қозғалыс мөлшері және күш импульсі
Нүкте қозғалысының негізгі динамикалық сипаттамаларының бірі – қозғалыс мөлшері.Нүктенің қозғалыс мөлшері деп оның массасы мен жылдамдық векторының көбейтіндісіне тең (mV) векторлық шаманы айтады. Қозғалыс мөлшерінің векторы әрқашан нүкте жылдамдығымен бағыттас болады. Белгілі уақыт аралығындағы күштің нүктеге әсерін күш импульсі дейді.Күштің элементар импульсі деп күш векторының элементар уақытқа көбейтіндісіне тең векторлық шаманы айтады: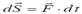 
Бұл вектор күштің әсер ету сызығының бойымен бағытталады.
56. Инерция күштері
Инерция күштері. 
актив күштері мен Rреакция күші әсер ететін материялық нүктені қарастырайық. Бұл нүкте үшін динамиканың негізгі заңы:
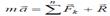түрінде жазылады. Соңғы өрнекті түрлендірейік:
Белгілеу енгізейік: 
векторы материялық нүктенің инерция күші деп аталады. Оның модулі нүктенің массасы мен үдеуінің көбейтіндісіне тең, ал бағыты үдеу векторына қарама-қарсы болады.
57. Нүкте қозғалысының дифференциалдық теңдеулері. Материялық нүктенің инерциялық санақ жүйесіндегі орнын rрадиус-векторымен анықтаймыз. Нүктеге әсер ететін күш жалпы жағдайда t уақытқа, нүктенің орнына, яғни r радиус-векторға және Vнүктенің жылдамдығына тәуелді бола алады, яғни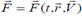 
Егер нүктенің үдеуі 
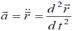ал жылдамдығы 
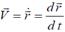екенін ескерсек, Ньютонның екінші заңы немесе нүкте динамикасының негізгі теңдеуі мына түрде жазылады 
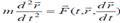Бұл теңдеу векторлық түрдегі нүкте қозғалысының дифференциалдық теңдеуі деп аталады.
58.Нүктенің абсолют, салыстырмалы және тасымал қозғалысы
. 
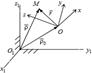Егер нүкте екі немесе одан артық қарапайым қозғалыстарға қатысса, онда нүктенің қозғалысын күрделі қозғалыс деп атаймыз.
Дененің МD нүктесінің қозғалысын М нүкте үшін тасымал қозғалыс деп атаймыз. М нүктенің D денеге немесе Oxyz жүйеге қатысты өз қозғалысын оның салыстырмалы қозғалысы дейміз. М нүктенің абсолют қозғалысы 
- радиус вектормен, “О” полюстің абсолют қозғалысы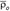 
- радиус вектормен, М нүктенің салыстырмалы қозғалысының 
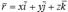радиус векторымен беріледі.
Жалпы жағдайда, МD нүкте “О” полюспен бірге ілгерілемелі және полюсқа қатысты айналма қозғалыста болады. Нүктенің абсолют қозғалысы 
теңдеуімен беріледі. Олай болса абсолют жылдамдық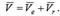 
Теорема. Нүктенің абсолют жылдамдығы оның тасымал және салыстырмалы қозғалыс жылдамдықтарының геометриялық қосындысына тең. Абсолют жылдамдықтың сан мәні (модулі) 
|
|
Дата добавления: 2017-01-14; Просмотров: 859; Нарушение авторских прав?; Мы поможем в написании вашей работы!