Примеры решения задач. Задача 7.1 Стенка холодильника, состоящая из наружного слоя изоляционного кирпича толщиной δ1=250 мм и внутреннего слоя совелита толщиной δ2 = 200

Задача 7.1 Стенка холодильника, состоящая из наружного слоя изоляционного кирпича толщиной δ₁=250 мм и внутреннего слоя совелита толщиной δ₂ = 200 мм, имеет температуру наружной поверхности t₁^ст=30°С и внутренней t₃^ст= –8°С. Коэффициенты теплопроводности материала слоев соответственно равны: λ₁=04 Вт/(м·К) и λ₂=0,09 Вт/(м·К). Определить плотность теплового потока через стенку и температурные градиенты в отдельных слоях. Представить графически распределение температуры по толщине стенки.

Исходные данные: δ₁=250 мм=0,25м; δ₂=200мм=0,2м; λ₁=0,24 Вт/(м·К); λ₂=0,09 Вт/(м·К); t₁^ст=30°С; t₃^ст=–8°С.

Определить: q; (gradt)₁; (gradt)₂.

Решение

1. Определяем плотность теплового потока через двухслойную плоскую стенку по формуле (3.7):

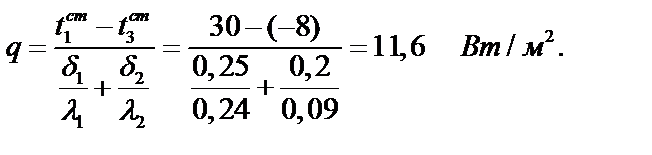
2. Находим температуру стенки на границе 1-го и 2-го слоёв:

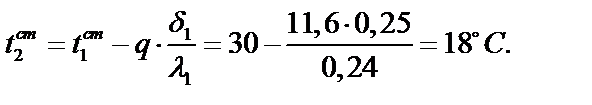
3. Вычисляем температурные градиенты в слоях стенки:

– в 1-м слое

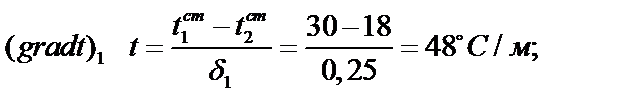
– в 2-м слое

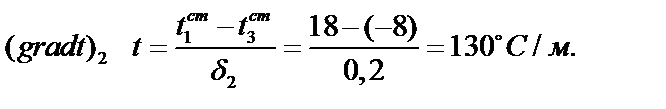
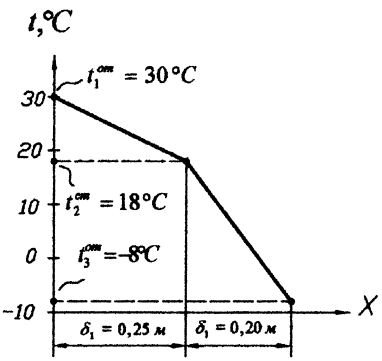
4. Строим график распределения температур по толщине стенки (см. рис. 3.10).

Рис. 3.10. Эпюра температур по толщине стенки

Задача 7.2 Горячий газ, омывающий снаружи тонкую стальную трубу, имеет среднюю температуру t_г и коэффициент теплоотдачи α₁; труба изнутри охлаждается воздухом со средней температурой t_в при давлении p₂ = 0,1 МПа. Определить скорость воздуха, обеспечивающую среднюю температуру стенки трубы не выше t₁; если внутренний диаметр трубы d₁, толщина ее δ и коэффициент теплопроводности λ = 20 Вт/(м · К).

Ответить на вопросы:

1. Какое из частных сопротивлений (1/α₁, δ/λ, 1/α₂) имеет большее влияние на величину коэффициента теплопередачи К в вашем варианте задачи?

2. Во сколько раз (примерно) нужно изменить коэффициент теплоотдачи α₂ в вашем варианте задачи, чтобы уменьшить температуру стенки t₁ в два раза? Покажите это на графике t = f(R). Как при этом изменится тепловой поток q?

Указание. При решении вопроса 2 можно считать стенку плоской.

Исходные данные: t_в=15°С; Р_в=0,1 МПа; d₁=200 мм=0,2 м; δ=8 мм=0,008 м; λ_ст=20 Вт/(м·К); t_r=650°С; α₁=50 Вт/(м²·К); t₁ =3 00°С.

Определить: величину w_в.

Решение

1. Определим теплофизические параметры воздуха при температуре t_в=15°С:

- коэффициент теплопроводности λ_ж = 0,0255 Вт/(м·К);

- коэффициент кинематической вязкости ν_ж = 14,6·10 ^–6 м²/с.

2. Определяем линейную плотность теплового потока, передаваемого от горячих газов к стене трубы:

q _l = α₁ · π · (d₁ + 2δ) (t_r– t_ст.ср.)=

=50 ·3,14 (0,2 + 0,016) (650 – 300) =11870 Вт/м.

3. Линейная плотность теплового потока между внутренней поверхностью трубы и нагреваемым воздухом равна

q _l = α₂ ·π · d₁ (t₁ – t_в),

откуда

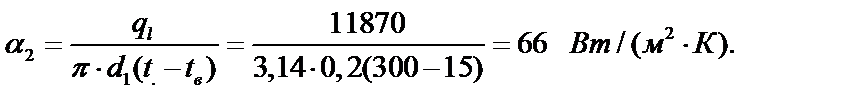
4. Определяем величину критерия Нуссельта для потока нагреваемого воздуха в трубе

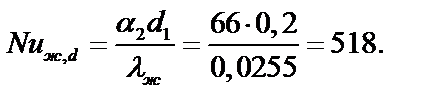
5. Для расчёта теплоотдачи при турбулентном вынужденном движении воздуха в трубе применим уравнение:

Nu_ж,d=0,018Re^0,8_ж,d,

откуда

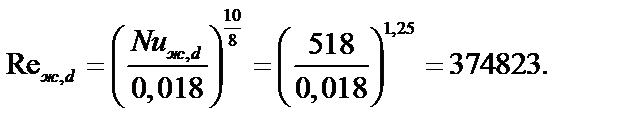
6. Находим скорость воздуха в трубе из уравнения:

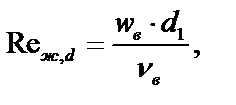
откуда

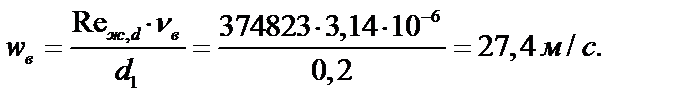
7. Считая стенку плоской, определим частные термические сопротивления процесса теплопередачи:

– сопротивление теплоотдачи от газов к стенке по формуле равно:

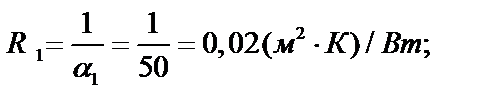
– термическое сопротивление стенки по формуле:

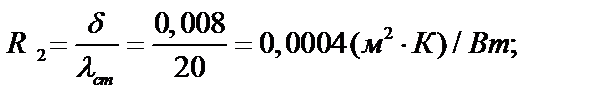
– сопротивление теплоотдачи от стенки к нагреваемому воздуху:

8. Построим график зависимости температуры t от частных термических сопротивлений (рис. 3.11).

Для этого по оси абсцисс отложим в выбранном масштабе величины частных термических сопротивлений R₁, R₂ и R₃, а по оси ординат – значения температур теплоносителей.

В результате получим линию ABC – эпюру температур в процессе теплопередачи от газов к воздуху при t₁ = 300°С.

9. Ответим на вопросы задания:

а) Какое из частных термических сопротивлений (R₁, R₂, R₃) имеет большее влияние на величину коэффициента теплопередачи?

Поформуле (3.32):

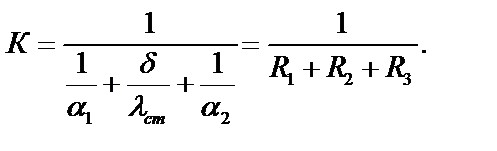
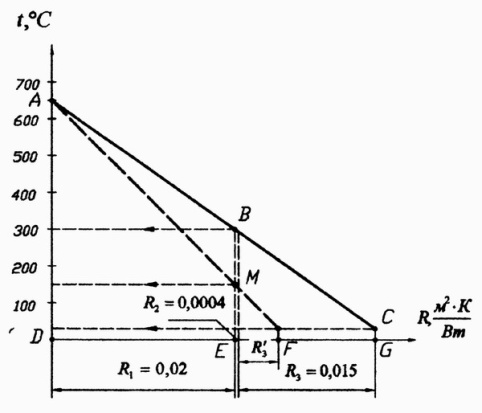
Рис. 3.11. Эпюра температур функции t=f(R) при теплопередаче

через стенку

Из сравнения этих величин видим, что наибольшие значения имеют R₁=0,02(м² ·К)/Вт и R₃=0,015(м² ·К)/Вт, поэтому они и вносят решающий вклад в величину К.

Термическое же сопротивление стенки R₂ меньше по величине примерно в 40-50 раз, поэтому практически не влияет на коэффициент теплопередачи.

б) Во сколько раз нужно изменить коэффициент теплоотдачи α₂, чтобы уменьшить температуру стенки t₁ в 2 раза?

Отложимнаграфикеотрезок:

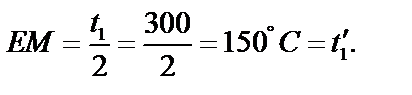
Проведём линию АМ и построим точку F на пересечении с осью абсцисс.

Отрезок ЕF нам даёт в масштабе величину R₃΄=0,005(м² ·К)/Вт.

Отсюда требуемый коэффициент теплоотдачи будет равен:

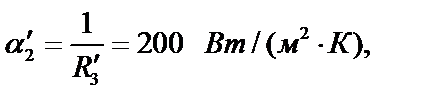
т.е. коэффициент теплоотдачи 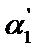нужно увеличить в 200/66≈3 раза.

Линейная плотность теплового потока в этом случае должна быть:

q΄ _l = α΄₂ · π ·d₁ (t΄₁ – t_в) = 200 · 3,14 · 0,2(150 – 15) = 16960 Вт/м.

Задача 7.3 Определить удельный лучистый тепловой поток q (в ваттах на квадратный метр) между двумя параллельно расположенными плоскими стенками, имеющими температуры t₁ и t₂ и степени черноты ε₁ и ε₂, если между ними нет экрана. Определить q при наличии экрана со степенью черноты ε_э (с обеих сторон).

Ответить на вопросы:

во сколько раз уменьшится тепловой поток, если принять в вашем варианте задачи ε_э = ε₁ по сравнению с потоком без экрана?

для случая ε₂ = ε₁ определите, какой экран из таблицы даст наихудший эффект и какой - наилучший.

Исходные данные: t₁=200°С; t₂=30°С; ε₁=0,52; ε₂=0,72; ε_э=0,02.

Определить: величины q_о и q_э.

Решение

1. Определяем величину теплового потока излучением между поверхностями (без экрана) по формуле (20.20):

.

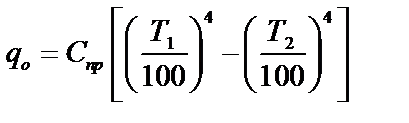Приведенный коэффициент излучения системы тел равен:

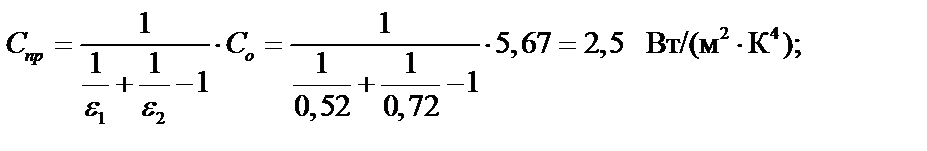
здесь С_о=5,67 Вт/(м²·К⁴) – коэффициент излучения абсолютно чёрного тела.

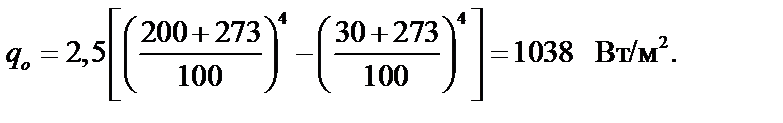
2. Находим лучистый тепловой поток между поверхностями q_э при установке полированного экрана со степенью черноты ε_э=0,02 с обеих сторон экрана.

Предварительно определим приведенный коэффициент излучения поверхностей и экрана:

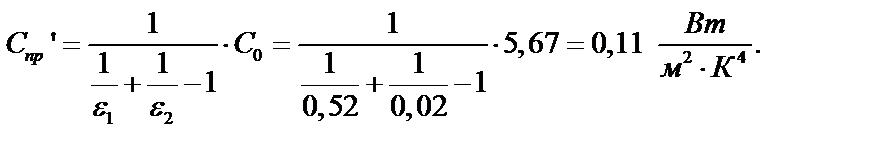
3. Рассчитываем лучистый поток между поверхностями при установке полированного экрана по формуле (20.25):

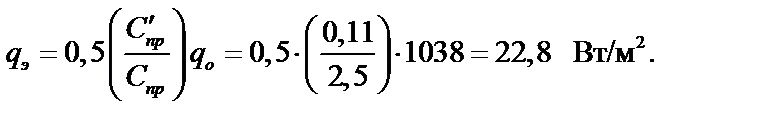
Отсюда следует, что установка одного полированного экрана уменьшает теплообмен излучения примерно в 45,5 раза и составляет 2,2% от величины теплообмена излучением без экрана.

4. Определим лучистый поток между пластинами при установке шероховатого экрана со степенью черноты ε_э=ε₁.

Приведенный коэффициент излучения пластины и экрана равен:

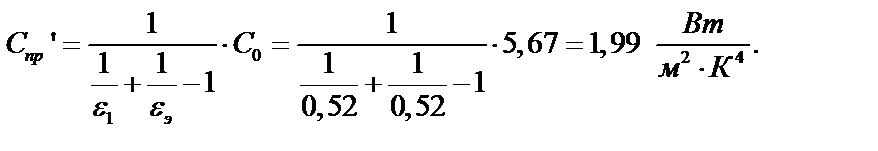
Лучистыйпотокравен:

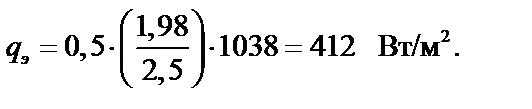
Таким образом лучистый поток между пластинами при применении шероховатого экрана уменьшается в 2,5 раза.

Задача 7.4 Определить поверхность нагрева водо-воздушного рекуперативного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если объемный расход воздуха при нормальных условиях V_н, средний коэффициент теплопередачи от воздуха к воде K, начальные и конечные температуры воздуха и воды равны, t^'_1, t^''₁, t^'_2, и t^''₂ соответственно. Определить также расход воды G через теплообменник.

Указание. Среднюю объёмную изобарную теплоёмкость воздуха принять равной C΄_pm=1,32 КДж/(м³·К).

Исходные данные: V_н·=500 м³/ч; К=21 Вт/(м²·К); t΄₁=500°С; t^΄΄₁=250°С; t΄₂=10°С; t^΄΄₂=90°С.

Определить: величины F и G_в.

Решение

Расчёт ведём для двух схем движения теплоносителя: прямоточной и противоточной.

I. Прямоток

1. Определяем объёмный расход греющего воздуха:

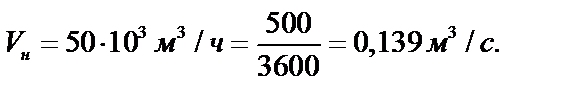
2. Находим количество тепла, передаваемого в теплообменнике от горячего воздуха к нагреваемой воде:

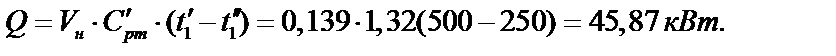
3. Определяем среднелогарифмический температурный напор:

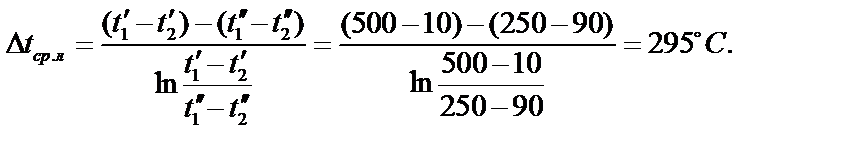
4. Поверхность нагрева теплообменного аппарата равна:

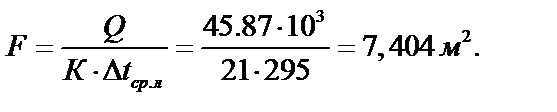
5. Расход охлаждающей воды равен:

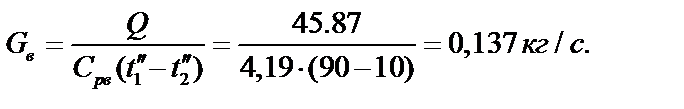
II. Противоток

1. Среднелогарифмический температурный напор равен:

Требуемая поверхность нагрева теплообменного аппарата равна:

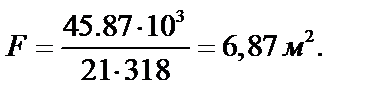
Дата добавления: 2017-01-14