Частица в одномерной прямоугольной яме

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида

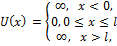
Где 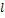- ширина «ямы», а энергия отсчитывается от ее дна

Уравнения Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения за пределами «ямы» равна нулю. На границах ямы непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

В пределах «ямы» уравнение Шредингера сведется к уравнению

или , где

Общее решение дифференциального уравнения

62.Прохождение частицы через прямоугольный потенциальный барьер.

Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях. Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U₀. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U₀, то с точки зрения классической физики она не может преодолеть его и отразится от него. Действительно, классическая физика требует безусловного сохранения энергии. Если представить, что частица с Е < U₀, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.

С точки зрения квантовой физики частица с Е < U₀ может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.
Вероятность прохождения частицы массы m через барьер D определяется соотношением

где .
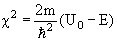Основная зависимость коэффициента прохождения D от ширины a и высоты барьера U₀ определяется экспоненциальным множителем e^-χa.

В случае a ~ 10^-13 см, m ~ 10^-24 г для (U₀ − E) ~ 10 МэВ D ~ 1/e.
То есть частица (протон, α-частица) с заметной вероятностью может пройти сквозь потенциальный барьер, превышающий её энергию на 5–10 МэВ.

Дата добавления: 2017-01-14