Уравнение Шредингера для атома водорода

Линейный гармонический осциллятор в квантовой механике.

Линейный гармонический осциллятор — система, совершающая одномерное движение под действием квазиупругой силы, — является моделью, используемой во многих задачах классической и квантовой теории. Пружинный, физический и мате­матический маятники — примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна:

где w ₀ — собственная частота колебаний осциллятора, т — масса частицы.

Зависи­мость имеет вид параболы (рис. 300), т. е. «потенциальная яма» в данном случае является параболической.

Гармонический осциллятор в квантовой механике — квантовый осциллятор — опи­сывается уравнением Шредингера:

(63.2)

где Е — полная энергия осциллятора.

В теории дифференциальных уравнений до­казывается, что уравнение (63.2) решается только при собственных значениях энергии

(63.3)

Формула (63.3) показывает, что энергия квантового осциллятора может иметь лишь дискретные значения, т. е. квантуется.

Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования. Квантование энергии возникает как естественное условие, появляющееся при решении уравнения Шредингера, в некотором смысле аналогичное причине квантования энергии для частицы в потенциальной яме. Применить стационарное уравнение Шредингера к атому водорода это значит:

а) подставить в это уравнение выражение для потенциальной энергии взаимодействия электрона с ядром

б) в качестве m подставить me - массу электрона

После этого получим уравнение Шредингера для атома водорода:

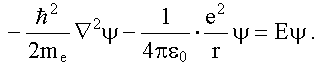
Так как потенциальная энергия зависит только от r, решение уравнения удобно искать в сферической системе координат: r, θ, φ.(рис. 8.1)

Рис. 8.1

Волновая функция в этом случае будет функцией от r, θ и φ, т.е.

Оператор Лапласа необходимо записать в сферических координатах, т.е. выразить через производные по r, θ и φ. Мы не будем этого делать, поскольку получение решения уравнения Шредингера для атома водорода не входит в программу курса общей физики. Приведем лишь результаты.

Оказывается, что решение уравнения Шредингера для атома водорода существует при следующих условиях:

а) при любых положительных значениях полной энергии (E > 0). Это так называемыенесвязанные состояния электрона, когда он пролетает мимо ядра и уходит от него на бесконечность;

б) при дискретных отрицательных значениях энергии

Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода. Целое число n называют главным квантовым числом.

Дата добавления: 2017-01-14