Квинтильный коэффициент

Децильный коэффициент

Все население подразделяется в зависимости от уровня дохода на 10 групп по 10% населения в каждой. Такие группы называют децили.

0 100% Д1 Д2 Д3 Д4 Д5 Д6 Д7 Д8 Д9 Д10

Децильный коэффициент рассчитывает как отношение пограничного значения между 9-м и 10-м децилями к пограничному значению дохода между 1-м и 2-м децилями. Он показывает, во сколько раз доходы 10% самой богатой части общества превышают доходы 10% его беднейшей части.

Коэффициент фондов

Рассчитывается как отношение среднего значения дохода между 9-м и 10-м децилями к среднему значению дохода между 1-м и 2-м децилями.

Рассчитывается по принципу децильного коэффициента, только общество делится на 5 групп (по 20%) по уровню дохода. Квинтильный коэффициент равен соотношению пограничного значения дохода между 4-м и 5-м квинтилями и пограничного значения дохода 1-м и 2-м квинтилями.

Квартильный коэффициент. Общество делится на 4 группы (по 25%) по уровню дохода. Квартальный коэффициент равен соотношению пограничного значения дохода между 3-м и 4-м квартилями и пограничного значения дохода между 1-м и 2-м квартилями.

42. Вариация. Абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

Показатели варьирования осредненных статистических признаков: размах вариации, среднее линейное отклонение, среднее кватратическое отклонение (дисперсия), коэффициент вариации. Расчетные формулы и порядок расчета показателей вариации.

Применение показателей вариации при анализе статистических данных в деятельности предприятий и организаций, учреждений БР, макроэкономических показателей.

Средний показатель дает обобщающий, типичный уровень признака, но не показывает степень его колеблемости, вариации.

Поэтому средние показатели необходимо дополнять показателями вариации. От размера и распределения от клонений зависит надежность средних показателей.

Важно знать основные показатели вариации, уметь правильно их рассчитывать и использовать.

Основными показателями вариации являются: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Формулы показателей вариации:

1. размах вариации.

X_μαχ - максимальное значение признака

X_min - минимальное значение признака.

Размах вариации может служить лишь приближенной мерой вариации признака, т.к. он исчисляется на основе двух крайних ее значений, а остальные во внимание не принимаются; при этом крайние значения признака для данной совокупности могут быть чисто случайными.

2. среднее линейное отклонение.

[X-X] - означает, что отклонения берутся без учета их знака.

Среднее линейное отклонение довольно редко используется в экономическом статистическом анализе.

3. Дисперсия.

4. Среднее квадратическое отклонение.

43. Способы расчёта дисперсии.

Дисперсия обладает рядом свойств (доказываемых в математической статистике), которые позволяют упростить расчеты.

1 способ. Дисперсия определяется как разность между средней квадратов вариантов и квадратом их средней:

(5.13)

2 способ. Способ отсчета от условного нуля или способ моментов. Используется при условии равных интервалов.

(5.14)

Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком (р), и доли единиц, не обладающих им(q):

(5.15)

44. Относительные показатели вариации: коэффициенты осцилляции, вариации.

• Коэффициент осцилляции
• Относительное линейное отклонение (линейный коэффициент варианции)
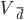
• Коэффициент вариации (относительное отклонение)

Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. Они вычисляются как отношения абсолютных показателей вариации к средней:

Коэффициент осцилляции
Относительное линейное отклонение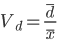
Коэффициент вариации

для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан

,

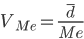так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.

В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где — средний квартиль полусуммы разности третьего (или верхнего) квартиля (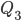) и первого (или нижнего) квартиля ().

.

45. Ряды динамики. Виды рядов динамики: моментные и интервальные; абсолютных, относительных величин, стационарные и нестационарные.

Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики (хронологические, временные), которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда и показатели времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени. Уровни ряда обычно обозначаются через «y», моменты или периоды времени, к которым относятся - через «t».

Существуют различные виды рядов динамики, которые классифицируют по следующим признакам:

• В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
• В зависимости от того выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определенные интервалы времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики.
• В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и неравноотстоящими уровнями во времени. Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называется равноотстоящими. Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются неравноотстоящими.
• В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные. Если математическое ожидание значения признака и дисперсия (основные характеристики случайного процесса) - постоянны, не зависят от времени, то процесс считается стационарным, и ряды динамики также называются стационарными. Экономические процессы во времени обычно не являются стационарными, т.к. содержат основную тенденцию развития, но их можно преобразовать в стационарные путем исключения тенденций.

Дата добавления: 2017-01-14