Определение необходимой численности выборочной совокупности

Для определения необходимой численности выборки нужно задать уровень точности выборочной совокупности с определённой вероятностью. В частности, необходимая численность случайной повторной выборки определяется по формуле , которая вытекает из формулы предельной ошибки: .

При проектировании выборочного наблюдения предполагаются заранее заданными величина допустимой ошибки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения . Величина , характеризующая дисперсию признака в генеральной совокупности, зачастую бывает неизвестна. Поэтому используют приближённые оценки генеральной дисперсии.

1. Исходя из результатов специально организованного пробного обследования (обычно небольшого объема), на базе которого определяется величина дисперсии признака, используемая в качестве оценки генеральной совокупности: ,

где 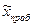– средняя арифметическая по результатам пробного обследования;

– число единиц, попавших в пробное обследование.

По данным нескольких пробных обследований выбирается наименьшее значение.

2. Опираясь на данные предыдущих обследований, как выборочных так и сплошных, проводившихся в аналогичных целях. Дисперсию изучаемого признака в выборке можно оценить по коэффициенту вариации, значение которого получено по итогам предшествующего сплошного или выборочного наблюдения. Коэффициент вариации v= 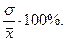Следовательно, дисперсия будет равна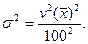

3. Зная примерную величину средней дисперсии, находят дисперсию из соотношения .

4. Если известны и , то можно определить среднее квадратическое отклонение в соответствии с правилом «трёх сигм»:

,

где 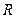– размах вариации.

Размах вариации при нормальном распределении примерно равен 6 (крайние значения отстоят в ту и другую сторону от средней на расстоянии 3 ).

Дата добавления: 2017-01-14