Универсальные конечные элементы балок-стенок, тонких плит и пологих оболочек (типы КЭ 11, 12, 21-24,27, 30, 41, 42, 44)

Предназначены для решения плоской задачи теории упругости, а также прочностного расчета тонких, жестких пластин и тонких пологих оболочек. Материал однородный по толщине элемента, линейно упругий изотропный.

Тонкими считаются пластины, у которых 5 £ Lmin/ d, где Lmin - наименьший из размеров в плане; d - толщина.

Жесткими считаются пластины, у которых наибольший прогиб не превышает d/5.

Оболочки считаются тонкими, если R/d > 20, где R - минимальный радиус кривизны срединной поверхности.

Оболочки считаются пологими, если L min/fo ³ 5, где fo - стрела подъема свода оболочки.

Применительно к решению плоской задачи теории упругости, МКЭ исходит из общепринятых гипотез об отсутствии деформаций (e_z, g_xz., g_yz = 0 для случаев плоской деформации) или напряжений (s_z, t_xz, t_yz = 0 для случая плоского напряженного состояния) в плоскостях, нормальных к срединной плоскости пластин. Функционал Лагранжа, как для плоской деформации, так и для плоского напряженного состояния имеет вид:

(1.6)

где: s_x,s_y,t_xy - нормальные и касательное напряжения;

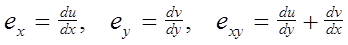-относительные линейные и угловая деформации;

u (x, у), v (x, у) - линейные смещения точек срединной плоскости по направлению осей Х и Y соответственно;

Px, Py — компоненты вектора внешней нагрузки по направлениям осей Х и Y соответственно;

W - двумерная область пластины.

При решении задач изгиба тонких пластин, МКЭ исходит из допущений (гипотез), принятых при построении инженерной теории тонких пластин, а именно:

· гипотезы о прямых нормалях Кирхгофа-Лява (е_xz = е_yz = 0);

· гипотезы о вертикальном смещении точек срединной плоскости пластины;

· гипотезы об отсутствии поперечного давления (s_z, = 0);

· плоское напряженное состояние.

Функционал полной потенциальной энергии изгибаемой пластины при таких допущениях и при нулевых граничных условиях имеет вид:

(1.7)

где: - погонные изгибающие моменты относительно осей Y и X, а также погонный крутящий момент, представляющие собой интегральные характеристики нормальных и касательного напряжений в направлении осей Х и Y:

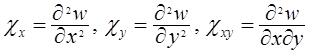- кривизны срединной поверхности в направлении осей Х и Y;

f(x,y) - функция внешней нагрузки, ортогональной к срединной поверхности пластины;

w(x,y) - функция прогибов по области срединной поверхности пластины;

Z -отрезок .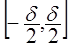

Относительные линейные и угловая деформации e_х,е_у,e_ху через кривизны запишутся следующим образом:

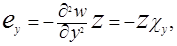(1.8)

Для плоского напряженного состояния деформации и напряжения связаны между собой зависимостями:

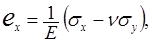
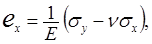(1.9)

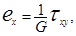
где: E - модуль Юнга; n - коэффициент Пуассона; G - модуль сдвига.

Для плоской деформации в (1.9) Е заменяется на Е/(1-ν²), ν -на ν/(1 - ν) и вычисляется σ_z= ν(σ_x+σ_y).

При расчете оболочечных конструкций целесообразно использовать КЭ нулевой кривизны (плоские КЭ) с независимой аппроксимацией нормального и тангенциальных перемещений, которым соответствуют функционалы потенциальной энергии, определяемые выражениями (1.6) и (1.7). Такой конечный элемент является простой комбинацией конечных элементов для плоского напряженного состояния и изгиба пластины с удовлетворением всех необходимых требований. Геометрические особенности оболочки учитываются геометрией вписанного многогранника. Поскольку со сгущением сетки увеличивается точность аппроксимации поверхности оболочки геометрией вписанного многогранника, то сходимость МКЭ в этом случае обеспечивается, что имеет теоретическое подтверждение.

При расчете плит и оболочек, лежащих на упругом основании, используется двухпараметрическая модель упругого основания П.Л. Пастернака, в которой две постоянные Cl и С2 характеризуют работу упругого основания на сжатие и срез (сдвиг). Если С2=0, получим однопараметрическую модель упругого основания Винклера.

Потенциальная энергия системы в этом случае

U = П+П₁ (1.10)

где:П — потенциальная энергия собственно конструкции, определяемая выражением (1.7), зависящим от типа конструкции;

П₁ — потенциальная энергия упругого основания, контактирующего с конструкцией, определяемая выражением

(1.11)

Допускается задание нагрузок на конечном элементе, как в местной, так и в общей системах координат с привязкой как в местной системе координат, так и в общей системе координат, а также с привязкой в виде приращений в общей системе координат.

Предусмотрены следующие виды нагрузок (табл.1.3):

5, 15 - сосредоточенная, задаваемая относительно осей местной или общей систем координат соответственно, с привязкой в местной системе координат;

6,16 - равномерно распределенная, задаваемая относительно осей местной и общей систем координат соответственно;

88 - температурное воздействие.

Таблица 1.3

Тип КЭ	Нагрузка	Схема и описание нагрузки	Информация, задаваемая в документах
6."Нагрузки"	7."Величины нагрузок"
Вид нагрузки	Направ-ление нагрузки	Величина нагрузки и привязка
21,22, 23,24, 27,30	Сосредо-точенная нагрузка в плоскости элемента XlO1Z1 (XlO1Y1)		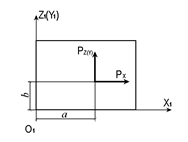	X Z	Рх(m),a(м),b(м) Рz(m),a(м),b(м)
41,42				X Y	Рх(m),a(м),b(м) Рy(m),a(м),b(м)
21,22, 23,24				X Z	Рх(m),a(м),b(м) Рz(m),a(м),b(м)
41,42,				X Y	Рх(m),a(м),b(м) Рy(m),a(м),b(м)
11,12 41,42,44	Сосредо-точенная нагрузка из плоскости элемента - силы и моменты			Z UX, UY	Рz(m),a(м),b(м) M(m м),a(м),b(м)
11,12 41,42,44				Z UX, UY	Рz(m),a(м),b(м) M(m м),a(м),b(м)
21,22, 23,24, 27,30	Равномерно распреде-ленная нагрузка в плоскости элемента		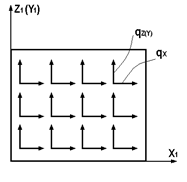	X Z	qx(m/м^2) qz(m/м^2)
41,42,				X Y	qx(m/м^2) qy(m/м^2)
21,23, 27,30		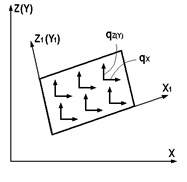		X Z	qx(m/м^2) qz(m/м^2)
41,44				X Y	qx(m/м^2) qy(m/м^2)
11,12 41,42,	Равномерно распреде-ленная нагрузка из плоскости элемента - силы и моменты по площади		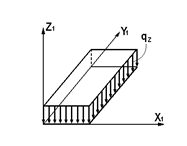	Z UX UY	qz(m/м^2) mx(mм /n.м) my(mм /n.м)
11,12 41,42,				Z UX UY	qz(m/м^2) mx(mм /n.м) my(mм /n.м)
11,12,21,22,23,24,27,30,41,42,44,					t, Dt, a
21.22.23,24,27,30				X Z	t, Dt, a1 t, Dt, a2
11,12				UX UY	t, Dt, a1 t, Dt, a2
41,42,				X,UX Y,UY	t, Dt, a1 t, Dt, a2

Дата добавления: 2017-01-14