Расчет на динамические воздействия

Задача динамического расчета формулируется, как и в статическом случае, в виде вариационного равенства

(3.1)

u(0)=и⁰, ∂u/∂t(0)=и¹, где

и_i = u (t ) - точное решение;

b(u,v), c(u,v) - возможные работы инерционных и демпфирующих сил,

и⁰,и¹ - начальные значения перемещения и скорости.

Остальные обозначения те же, что и в статической задаче.

Реализован метод решения динамической задачи, заключающийся в сочетании МКЭ с разложением по формам собственных колебаний. Решение (2.1) ищем в виде

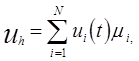(3.2)

где : u_i (t) - скалярные функции;

m _i - базисные функции соответствующей статической задачи.

Подставив в (3.1) U_h вида (3.2) вместо U и m_j (j=1.......N ) вместо V, получим систему обыкновенных дифференциальных уравнений

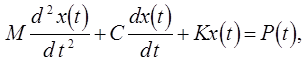(3.3)

где: х(t), x⁰, x¹ - векторы с элементами Xi(t)=u_i(t), x_i ⁰ = L_iU ^u, x_i ¹=LiU¹,

M и С - матрицы масс и демпфирования с элементами т_i,j=b(m_i , m_j), c_i,j = c(m_i , m_j).

Матрица жесткости К и вектор нагрузок P(t) определяются, как и для статической задачи. Этот метод известен как полудискретная аппроксимация. Его погрешность (разность между U и U_h)по потенциальной и кинетической энергии оценивается как в совместном, так и в несовместном случаях величиной, пропорциональной h^t.

Систему (3.3) решаем методом разложения по формам собственных колебаний.

Пусть l_i., j_i <M j_i, j_i >=1 решение задачи на собственные значения

Кj =lMj (3.4)

(Символом <,> обозначается скалярное произведение в R ^N).

Задача на собственные значения (3.4) решается методом итерации подпространств.

Полагая в (3.3) из ортогональности функции j_i получим (при определенных предположениях относительно матрицы С), что система (3.3) распадается на независимые уравнения относительно y_i (t):

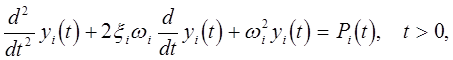
(3.5)

где:

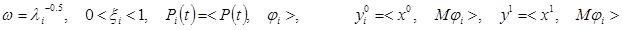
Решение уравнения (3.5) имеет вид:

где

Векторы инерционных сил S_i(t) вычисляются по формуле

В расчетах используются величины

1. Для ветровой нагрузки S_i,0 = w_н g_i,

где w_н - нормативное значение ветровой нагрузки,

g _i - коэффициент динамичности, зависящий от w _i, x _i и скорости ветра.

2. Для сейсмической нагрузки

где А - относительная величина ускорения,

b _i - коэффициент динамичности, зависящий от w _i и x _i.

3. Для импульсивной и ударной нагрузок

где e _i, зависит от t_o , w _i

t_o - время действия импульса;

y - учитывает периодичность действия нагрузки;

, где

m₀, n₀ - масса и скорость ударяющего тела;

n - коэффициент восстановления формы соударяющихся тел.

Коэффициент y зависит от того, являются ли колебания установившимися или неустановившимися 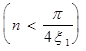, где n - число повторении импульсов.

4. Для гармонической нагрузки вычисляются суммарные по всем формам инерционные силы S ₁ и S ₂ , соответствующие косинусоидальной (действительной) и синусоидальной (мнимой) составляющим:

где

.

Тогда

В перечисленных выше вариантах воздействий возможно точное вычисление y_i (t ). В остальных случаях решения y_i (t ) находим численно.

В частности, при расчете на сейсмическую нагрузку по акселерограмме в каждый момент времени t _k задается вектор P_k. =P(t_k). Тогда в (3.5) имеем P_i,k =P_i(t_k ).

Далее уравнения (3.5) решаются методом конечных разностей по схеме Ньюмарка. Получаем значения перемещений y_i,k = y_i (t_k) и инерционных сил S_i,k = S_i (t_k), по которым вычисляется

При расчетах на сейсмические воздействия ПК ЛИРА позволяет применить метод спектра ответов. Расчет заключается в том, чтобы при заданной функции S₀(ω), обычно кусочно-линейной, вычислить линейной интерполяцией значения S₀(ω_i). Функция S₀(ω) может быть представлена графиками спектров ускорений, скоростей или перемещений.

Реализованы следующие модули расчета на динамические воздействия:

Модуль 20 - сейсмическое воздействие по СНиП II-7-81;

Модуль 30 - сейсмическое воздействие по СНиП II-7-81*

с изменениями на 01.01.1996 года;

Модуль 35 - сейсмическое воздействие по СНиП II-7-81**

с изменениями на 01.01.2000 года;

Модуль 27 - сейсмическое воздействие по акселерограмме;

Модуль 32 - сейсмическое воздействие по СНРА II-2.02-94 (Армения);

Модуль 33 - сейсмическое воздействие по нормам

КМК 2.01.03-96 (Узбекистан);

Модуль 40 - сейсмическое воздействие по NF P 06-013 (Франция);

Модуль 41 - сейсмическое воздействие по методу спектра ответов;

Модуль 42 - сейсмическое воздействие по IBC-2000 (США);

Модуль 21 – ветровое воздействие с учетом пульсации

по СНиП 2.01.07-85*;

Модуль 22 – импульсивное воздействие;

Модуль 23 – ударное воздействие;

Модуль 24 – гармонические колебания;

Модуль 28 – гармонические колебания с учетом частотных зон;

Модуль 100 – модальный анализ.

Дата добавления: 2017-01-14