Расчет физически нелинейных задач

Общие положения

РЕШЕНИЕ НЕЛИНЕЙНЫХ ЗАДАЧ

Нелинейный процессор предназначен для решения физически и геометрически нелинейных, а также контактных задач.

В линейных задачах существует прямая пропорциональность между нагрузками и перемещениями вследствие малости перемещений, а также между напряжениями (усилиями) и деформациями в соответствии с законом Гука. Поэтому для линейных задач справедлив принцип суперпозиции и независимости действия сил.

В физически нелинейных задачах отсутствует прямая пропорциональность между напряжениями и деформациями. Материал конструкции подчиняется нелинейному закону деформирования. Закон деформирования может быть симметричным и несимметричным – с различными пределами сопротивления растяжению и сжатию.

В геометрически нелинейных задачах отсутствует прямая пропорциональность между деформациями и перемещениями. На практике наибольшее распространение имеет случай больших перемещений при малых деформациях.

В задачах конструктивной нелинейности имеет место изменение расчетной схемы по мере деформирования конструкции, например, в момент достижения некоторой точкой конструкции определенной величины перемещения возникает контакт этой точки с опорой.

Для решения таких задач нелинейный процессор организует процесс пошагового нагружения конструкции и обеспечивает решение линеаризованной системы уравнений на каждом шаге для текущего приращения вектора узловых нагрузок, сформированного для конкретного нагружения.

При решении задач конструктивной нелинейности применяется шагово-итерационный метод.

Нелинейный процессор позволяет получить напряженно-деформированное состояние для мономатериальных и для биматериальных, в частности железобетонных, конструкций.

Для решения нелинейных задач необходимо задавать информацию о количестве шагов и коэффициентах к нагрузке. Схема может содержать несколько нагружений, из которых может быть сформирована последовательность (история) нагружений.

Моделирование физической нелинейности материалов конструкций производится с помощью физически нелинейных конечных элементов, воспринимающих информацию из развитой библиотеки законов деформирования материалов (зависимостей σ-ε). Библиотека законов деформирования позволяет учитывать практически любые физически-нелинейные свойства материала. Эта библиотека законов деформирования материала является библиотекой открытого типа и может пополняться новыми законами.

Шаговый процессор позволяет получить напряженно-деформированное состояние с учетом нелинейных эффектов как для мономатериальных, так и для биматериальных конструкций. Для последних предлагается определенный набор характеристик второго материала (армирующих включений).

Библиотека физически нелинейных конечных элементов содержит также элементы, позволяющие моделировать одностороннюю работу твердого тела и сыпучей среды - грунта на сжатие с учетом сдвига по схеме плоской деформации в соответствии с законом Кулона.

Матрица жесткости линеаризованной физически нелинейной системы формируется на основании переменных интегральных жесткостей, вычисляемых в точках интегрирования конечного элемента при решении упругой задачи на конкретном шаге. Схема численного интегрирования по области конечного элемента и набор используемых жесткостей определяются типом конечного элемента. Для того чтобы получить соответствующий набор интегральных жесткостей, сечение конечного элемента в точках интегрирования дробится на ряд элементарных подобластей. В центрах этих подобластей определяются новые значения физико-механических характеристик материала в соответствии с заданной диаграммой деформирования. На каждом шаге решается линеаризованная задача с формированием векторов перемещений, усилий и новых интегральных жесткостей по касательному модулю для последующего шага. Количество шагов и коэффициенты к нагрузке задаются пользователем. Геометрическая интерпретация шагового метода для случая одноосного растяжения (сжатия) представлена на рисунке 7.1.

Рис. 7.1

Шаговый процессор позволяет комбинировать линейные и нелинейные конечные элементы. Допускается расчет по суперэлементной схеме, если нелинейные элементы присутствуют только в основной схеме.

На каждом шаге производится оценка напряженно-деформированного состояния. В разделе результатов расчета «Сведения о состоянии материалов» приводятся сообщения о развитии или достижении предельных состояний, появлении пластических шарниров или состояний разрушения.

Для стержневых конечных элементов анализируется напряженно-деформированное состояние поперечных сечений стержня в точках дробления. Напряженно-деформированное состояние в плоских и объемных конечных элементах анализируется в центральной точке элемента.

Библиотека физически-нелинейных КЭ содержит элементы, позволяющие производить статический анализ конструкций, состоящих из разнородных конечных элементов, с учетом физической нелинейности материала. Состав библиотеки приведен в табл. 7.1.

Таблица 7.1.

№№ КЭ	Наименование КЭ	Признак схемы	Плос-кость располо-жения	Степени свободы
(205)	Универсальный пространственный стержневой конечный элемент - суперэлементного построения Универсальный пространственный стержневой конечный элемент - равновесного построения		XOZ XOZ XOY произ-вольно	X, Z X, Z, UY   X,Y,Z X,Y,Z UX, UY, UZ
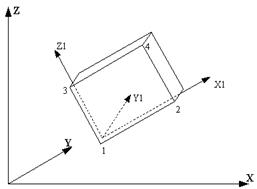
221 (223)	Прямоугольный элемент балки -стенки	1,2,5 (4,5)	XOZ (произ-вольно)	X, Z (X,Y,Z)
222 (224)	Треугольный элемент балки-стенки	1,2,5 (4,5)	XOZ (произ-вольно)	X, Z (X,Y,Z)
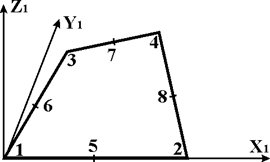
(227)	Четырехугольный (8-узловой) элемент балки-стенки	(4,5)	XOZ (произ-вольно)	X, Z (X, Y, Z)
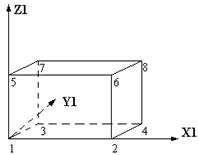
	Параллелепипед		произ-вольно	X, Y, Z
	Тетраэдр	4, 5	произ-вольно	X, Y, Z
	Прямая треугольная призма		произ-вольно	X, Y, Z
	Пространственный 6-ти узловой изопараметрический элемент (произвольная треугольная призма)		произ-вольно	X, Y, Z
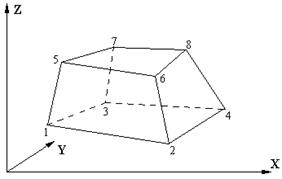
	Пространственный 8-ти узловой изопараметрический элемент (произвольный гексаэдр)		произ-вольно	X, Y, Z
	Прямоугольный элемент оболочки		произ-вольно	X, Y, Z, UX, UZ, UY
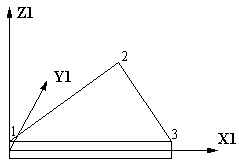
	Треугольный элемент оболочки		произ-вольно	X,Y,Z UX,UY,UZ
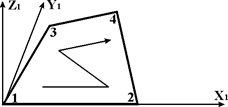
	Универсальный четырехугольный конечный элемент оболочки		произ-вольно	X, Y, Z, UX, UY, UZ
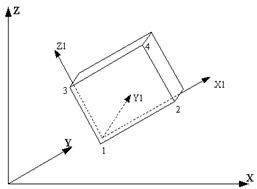
	Прямоугольный элемент грунта (плоская деформация)	1,2	XOZ	Плоская деформация X, Z
	Треугольный элемент грунта (плоская деформация)	1,)	XOZ	Плоская деформация X, Z
	Четырехугольный элемент грунта (плоская деформация)		XOZ	Плоская деформация X, Z

Дата добавления: 2017-01-14