Визначники. Їх обчислення

Матриці. Операції над матрицями.

Елементи лінійної алгебри

Прямокутна таблиця чисел a _ij (i = 1÷m, j = 1÷ n), що складається з m рядків та n стовпців,

називається матрицею. Коротко матрицю позначають так: А = {a_ij }_m·n, де a_ij - елементи матриці, причому і – номер рядка, j – номер стовпця, на перетині яких стоїть даний елемент.

Добуток m ∙ n називається розміром матриці. Якщо m = n, то мова йде про квадратну матрицю.

Для матриць визначені наступні операції:

1) aлгебраїчне додавання. Нехай А = {a_ij}_{m ∙ n}, В = {b_ij }_{m ∙ n}, тоді С =А + В,

де С = {c_ij }_{m ∙ n} та c_{ij =}а _ij + b_ij.

2) множення матриці на число. Нехай А = {a_ij }_{m ∙ n}, l = const ≠ 0. Тоді С = l ∙ А,

де С = {c_ij }_{m ∙ n} та c_ij = l ∙ a_ij.

3) добуток матриць. Нехай А = {a_ij }_{m ∙ n},, В = {b_ij }_{n ∙ р}. Тоді С = А ∙ В = {c_ij }_{m ∙ р,}

де c_ij = 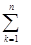a_ik ∙ b_kj та i =1¸m, j = 1÷ р.

Детермінантом (визначником) n – го порядку є число, що ставиться у відповідність квадратній матриці А розміру n ∙ n. Позначається: det A або ∆А.

Розглянемо окремі випадки обчислення визначників.

Нехай n = 2 (визначник другого порядку):

а₁₁ а₁₂

∆ = а₂₁ а₂₂ = а₁₁ а₂₂ - а₁₂ а_21.

Нехай n = 3 (визначник 3 – го порядку):

а₁₁ а₁₂ a₁₃

∆ = а₂₁ а₂₂ a₂₃ = а₁₁ а₂₂ a₃₃ + а₁₂ a₂₃ a₃₁ + а₂₁ a₃₂ a₁₃ - a₁₃ а₂₂ a₃₁ - a₂₃ a₃₂ а₁₁ -

a₃₁ a₃₂ a₃₃ - а₂₁ a₁₂ a₃₃

Ця сума може бути легко утворена, якщо застосувати „правило трикутників”:

· · · · · · · · · · · · · · · · · ·

∆ = · ·· + · · + · · · − · · · − · · · − · · ·

· · · · · · · · · · · · · · · · · · ∑

Мінором М_ij елемента а _ij матриці називається визначник, який утворюється з даного визначника в результаті викреслення і – го рядка та j-го стовпця.

Алгебраїчним доповненням А _ij елемента а _ij називається його мінор, взятий зі знаком (-1) ^i+j,

тобто А _ij =(-1) ^i+j М _ij.

Теорема 1. Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх aлгебраїчні доповнення.

Властивості визначників:

1) визначник не зміниться, якщо його рядки замінити відповідними стовпцями;

2) якщо переставити місцями два рядки (стовпці),то визначник поміняє знак;

3) якщо один з рядків (стовпців) визначника складається тільки з нулів, то визначник дорівнює нулю;

4) якщо визначник має два однакові рядки (стовпці), то він дорівнює нулю;

5) спільний множник, що міститься в усіх елементах одного рядка (стовпця), можна винести за знак

визначника;

6) якщо у визначнику елементи двох рядків (стовпців) пропорційні, то визначник дорівнює нулю;

7) визначник не зміниться, якщо до елементів одного рядка (стовпця) додати відповідні елементи

іншого рядка (стовпця), помножені на одне й те саме число, відмінне від 0.

Дата добавления: 2017-01-14