Алгоритм получения случайной величины, распределенной по Пуассону

Алгоритм получения значения нормально распределенной случайной величины

Нормальное распределение является наиболее часто встречающимся. Функция плотности распределения вероятностей для него имеет вид:

где m – математическое ожидание, а 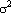– дисперсия. Согласно центральной предельной теореме теории вероятностей СВ

распределена асимптотически нормально, если 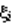распределены одинаково.

Для практического получения значений 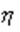в качестве и выбирают равномерно распределенные СВ. При этом наиболее часто используют преобразование

(8)

где x_i – равномерно распределенные на (0,1) случайные числа. При к=12 формула приобретает вид наиболее удобной для расчетов, но она дает достаточно точные результаты уже для к=3,4. Формула (8) верна для центрированной (m=0) и нормированной ( =1) случайной величины.

Для получения y*, распределенного нормально с произвольными m и 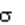, пользуются дополнительно преобразованием

y^*=m + 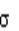y (9)

Закон Пуассона описывает число событий, происходящих за одинаковые промежутки времени, при условии независимости этих событий. Это распределение хорошо описывает количество вызовов телефонной станции за определенное время суток, заказов такси и т.д. Закон Пуассона называют законом появления редких событий.

В основе алгоритма получения случайных чисел, распределенных по Пуассону лежит предельная теорема Пуассона. В соответствии с этой теоремой, если n – количество событий велико, а р – вероятность успеха мала, то вероятность того, что при n испытаниях событие произойдет к раз равна:

Здесь np=а, где а – параметр закона Пуассона.

Процедура получения чисел, распределенных по Пуассону заключается в следующем:

1. Положить р меньше, либо равно 0,1 (так как события являются редкими).

2. Вычислить число испытаний n=а/р.

3. Значение х – случайного числа с равномерным на интервале (0,1) законом распределения сравнить с р, если х меньше, либо равно р, то к счетчику событий добавляется 1.

4. Проводится n испытаний, после чего содержимое счетчика можно считать случайным числом, распределенным по Пуассону.

Аналогично можно получить значения случайных величин, распределенных в соответствии с геометрическим, биноминальным и другими распределениями дискретных случайных величин

Лекція 2.3. Метод аналітичних перетворень. Алгоритм отримання значень системи дискретних випадкових величин.

Алгоритмы получения значений систем случайных величин (случайных векторов)

Дата добавления: 2017-01-14