
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод разложения по координатным случайным величинам
|
|
|
|
Метод аналитических преобразований
Пусть системы непрерывных случайных величин (СНСВ) 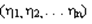 задана условными законами распределения СВ
задана условными законами распределения СВ  i (i=1,n). По теореме умножения плотностей распределения совместная функция плотности распределения вероятностей
i (i=1,n). По теореме умножения плотностей распределения совместная функция плотности распределения вероятностей
f(z1, z2,... zn)=f1(z1) f2(z2|z1) f3(z3|z1z2)... fn(zn| z1,z2, ..., zn-1).
Для системы двух случайных величин (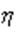 1,
1, 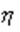 2), алгоритм получения вектора ее значений сводится к следующему:
2), алгоритм получения вектора ее значений сводится к следующему:
1. Вычисление частной функции плотности для  1:
1:
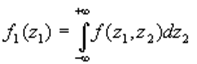
2. Получение значения  1 в соответствии с f1(z1) согласно любому методу, например, одному из описанных в предыдущем разделе 3.
1 в соответствии с f1(z1) согласно любому методу, например, одному из описанных в предыдущем разделе 3.
3. Вычисление частной функции плотности для второй компоненты  2 системы. Она может быть получена на основании теоремы умножения законов распределения:
2 системы. Она может быть получена на основании теоремы умножения законов распределения:

4. Получение  2 – значения
2 – значения 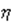 2 любым известным методом в соответствии с найденным законом ее распределения.
2 любым известным методом в соответствии с найденным законом ее распределения.
Алгоритм может быть обобщен для любого n. Однако, практические работы, выполняемые по этому методу, связаны с большими вычислительными трудностями, за исключением тех редких случаев, когда интегралы берутся. Поэтому разработаны другие методы, позволяющие решать задачу получения значений СНСВ.
Пусть СНСВ задана в рамках теории корреляций: математическими ожиданиями компонент (m1, m2, ... mn) и матрицей корреляционных моментов:
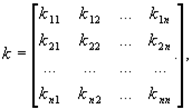

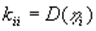
Доказано, что h i  можно получить с помощью их разложения по координатам СВ x i
можно получить с помощью их разложения по координатам СВ x i 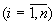 :
:
 (10)
(10)
где  i - некоррелированные, центрированные, нормированные нормально распределенные СВ.
i - некоррелированные, центрированные, нормированные нормально распределенные СВ.
Коэффициенты сij 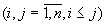 могут быть достаточно просто получены решением системы уравнений:
могут быть достаточно просто получены решением системы уравнений:
 ,
, 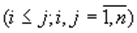 (11)
(11)
Алгоритм получения значений СНСВ сводится к следующему:
1. Решение системы нелинейных уравнений (11).
2. Получение n значений yi нормировнных, центрированных СВ, распределенных нормально.
3. Вычисление zi i=(1,n) значений СВ, образующих СНСВ в соответствии с (10).
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 287; Нарушение авторских прав?; Мы поможем в написании вашей работы!