Основные понятия марковских процессов

Моделирование экономических систем с использованием марковских случайных процессов

Алгоритм получения значений системы дискретных случайных величин

Дискретный двумерный вектор CDCB задается двумерным законом распределения, т.е.

а) матрицей вероятностей 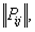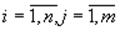, где Pij – вероятность совместного появления i-ого и j-ого значений соответственной первой и второй компоненты, причем: .

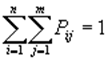б) двумя векторами возможных значений первой и второй компоненты {A_i}, {B_i}, .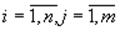

Получение значений двумерной дискретной системы случайных величин (СДСВ) может осуществляться по следующему алгоритму.

1. Вычисляют суммы , .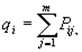

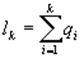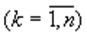2. Если х - равномерно распределенное случайное число из интервала (0,1) такое, что 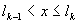, то считают, что ₁ компонента двумерной СДСВ получила к-ое значение.

3. Выбирают к-ую строку 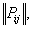вычисляют .

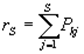4. Если вновь полученное с помощью датчика случайных чисел х такое, что вторая компонента СДСВ получила S-е значение.

5. Замечание: В алгоритме используется правило “розыгрыша по жребию”, однако надо иметь в виду, что .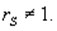

Функция ДО называется случайной, если ее значение при лю­бом аргументе / является случайной величиной.

Случайная функция ДО, аргументом которой является время, называется случайным процессом.

Марковские процессы являются частным видом случайных про­цессов. Особое место марковских процессов среди других классов случайных процессов обусловлено следующими обстоятельствами: для марковских процессов хорошо разработан математический ап­парат, позволяющий решать многие практические задачи; с помо­щью марковских процессов можно описать (точно или приближен­но) поведение достаточно сложных систем.

Определение. Случайный процесс, протекающий в ка­кой-либо системе S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для любого момента времени t₀ вероятность любого состояния системы в будущем (при t > t₀) зависит, только от ее состояния в настоящем (при t = t₀) и не зависит от того, когда и каким об­разом система S пришла в это состояние.

Классификация марковских процессов. Классификация марков­ских случайных процессов производится в зависимости от непре­рывности или дискретности множества значений функции X(t) и параметра t.

Различают следующие основные виды марковских случайных процессов:

• с дискретными состояниями и дискретным временем (цепь Маркова);

• с непрерывными состояниями и дискретным временем (мар­ковские последовательности);

• с дискретными состояниями и непрерывным временем (не­прерывная цепь Маркова);

• с непрерывным состоянием и непрерывным временем.

В данной работе будут рассматриваться только марковские про­цессы с дискретными состояниями S₁, S₂,..., S_n.

Граф состояний. Марковские процессы с дискретными состоя­ниями удобно иллюстрировать с помощью так называемого графа состояний (рис. 2.1), где кружками обозначены состояния S₁, S₂... системы S, а стрелками — возможные переходы из состо­яния в состояние. На графе отмечаются только непосредственные переходы, а не переходы через другие состояния. Возможные за­держки в прежнем состоянии изображают «петлей», т. е. стрелкой, направленной из данного состояния в него же. Число состояний системы может быть как конечным, так и бесконечным (но счет­ным). Пример графа состояний системы Ј представлен на рис.2.1.

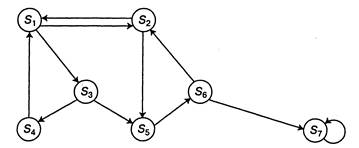
Рис. 2.1. Граф состояний системы S

Дата добавления: 2017-01-14