Краткие теоретические сведения. Методические указания к решению задачи №1

Методические указания к решению задачи №1

К решению задачи следует приступить после изучения тем «Основные понятия и аксиомы статики» и «Плоская система сходящихся сил».

Статика изучает общие свойства сил и условия равновесия твердых тел. находящихся под действием приложенных к ним сил.

Под равновесием твердого тела в статике понимается состояние покоя твердого тела,

При решении большинства задач механики приходится иметь дело с телами несвободными, т. е. лишенными возможности перемещаться в направлении действия приложенных к ним активных сил.

Тела, ограничивающие движение рассматриваемого твердого тела, называются связями. Сила, с которой связь действует на тело, препятствуя его перемещению, называется силой реакции связи.

Направления реакций основных типов связей показаны на рисунке 1.

а) реакция плоскости

б)реакция стержня

в) реакция гибкой связи

г) реакция цилиндрического шарнира

Рисунок 1

Согласно принципу освобождаемости от связей всякую связь молено отбросить, заменив ее реакцией.

Две и более силы, действующие на тело одновременно называются системой сил.

Система сил, линии действия которой лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.

Плоская система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме всех сил системы.

Условие равновесия плоской системы сходящихся сил; для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю.

, т.е.

При решении задачи векторное сложение сил заменяют сложением проекций сил на оси плоской системы координат.

Проекция силы - скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца силы на ось. Проекция силы считается положительной (+), если между направлением силы и направлением оси угол от 0° до 90° (рисунок 2а,2б), отрицательной (-), если между направлением силы инаправлением оси угол от 90°до 180° (рисунок 2в) и проекция силы на ось считается равной нулю, если сила перпендикулярна оси (рисунок2г).

Рисунок 2

Для равновесия твердого тела, находящегося под действием плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил системы на каждую из осей координат равнялась нулю:

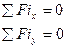
В задаче №1 рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом к шарниру "В" в каждой задаче приложены четыре силы, из которых две неизвестны. Решение задачи удобно выполнять аналитическим методом.

Последовательность решения задачи:

1. Выбрать тело (точку), равновесие которого следует рассматривать.

2. Освободить тело (шарнир В) от связей, заменив их реакциями.

3. Выполнить расчетную схему, на которой к шарниру В приложить все активные силы и реакции отброшенных связей.

4. Выбрать оси координат и составить уравнения равновесия;

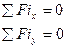
Выбирая оси координат, следует учитывать, что уравнения будут решаться проще, если одну из осей направить по неизвестной силе.

5. Определить реакции стержней из решения системы уравнений.

6, Проверить правильность полученных результатов, решив уравнения равновесия относительно заново выбранных осей координат.

Пример 1. Определить реакции стержней, удерживающих грузы и (рисунок 3). Массой стержней пренебречь.

Решетие:

1. Рассмотрим равновесие шарнира В (рисунок 3).

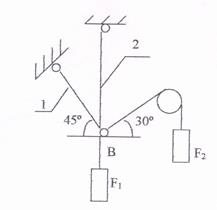
Рисунок 3

2. Освобождаем шарнир "В" от связей и изображаем действующие на него активные силы и реакции связей - составляем расчетную схему (рисунок 4).

Рисунок 4 - Расчетная схема

3. Выбираем систему координат, совместив ось "у" по направлению с реакцией R.2 и составляем уравнения равновесия для системы сил, действующих на шарнир "В":

(1)

(2)

4. Определяем реакции стержней и 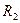, решая уравнения (1) и (2). Из уравнения (1):

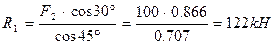
Подставляя найденное значение в уравнение (2), получаем;

Знак минус перед значением 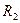указывает на то, что первоначально выбранное направление реакции неверное - следует направить реакцию 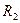в противоположную сторону, т.е. к шарниру В.

5. Проверяем правильность полученных результатов, выбрав новое направление осей координат х и у (рисунок 5).

Рисунок 5 - Расчетная схема

Относительно этих осей составляем уравнения равновесия.

(3)

(4)

Из уравнения (З) находим .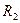

Подставляя найденное значение 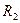в уравнение (4), получаем.

Значения реакций и 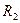, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Дата добавления: 2017-01-14