
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Краткие теоретические сведения. Методические указания к решению задачи № 4
Методические указания к решению задачи № 4
К решению задачи следует приступать после изучения темы "Кручение".
Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент.
Крутящий момент ( )- есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в сечении. Крутящий момент равен алгебраической сумме внешних скручивающий или вращающих моментов, приложенных к брусу справа или слева от сечения.
)- есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в сечении. Крутящий момент равен алгебраической сумме внешних скручивающий или вращающих моментов, приложенных к брусу справа или слева от сечения.

Определяют крутящий момент в сечении методом сечений, изученным в теме "Растяжение и сжатие".
При кручении в любом поперечном сечении бруса возникают только касательные напряжения  , измеряемые в МПа,
, измеряемые в МПа,
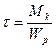
где  - крутящий момент в сечении, Н-м;
- крутящий момент в сечении, Н-м;
 - полярный момент сопротивления кручению, мм3.
- полярный момент сопротивления кручению, мм3.
Полярный момент сопротивления ( ) - это геометрическая характеристика сечения. Он характеризует способность сечения сопротивляться образованию деформации кручения.
) - это геометрическая характеристика сечения. Он характеризует способность сечения сопротивляться образованию деформации кручения.
Полярные моменты сопротивления простых сечений можно определить по формулам:
1) сечение в форме круга, с диаметром d:

2) сечение в форме кольца, с внутренним диаметром d и наружным диаметром D:

где 
Условие прочности при кручении:
 ,
,
где  - допускаемое напряжение при кручении.
- допускаемое напряжение при кручении.
В соответствии с условием прочности можно выполнять проектный или проверочный расчет.
Проектный расчет заключается в определении из условия прочности поперечных размеров бруса.
Последовательность решения задачи:
1. Разделить брус на участки по поперечным сечениям, в которых приложены внешние скручивающие моменты или изменяются размеры поперечного сечения.
2. Методом сечений определить величину внутренних крутящих моментов «  » на каждом участке и по результатам вычислений построить эпюру крутящих моментов.
» на каждом участке и по результатам вычислений построить эпюру крутящих моментов.
3. По эпюре крутящих моментов определяют опасное сечение бруса и наибольший по модулю крутящий момент  , выразив его в
, выразив его в  .
.
4. Из условия прочности при кручении и пользуясь формулами для полярных моментов сопротивления простых сечений подбирают размеры поперечного сечения бруса:
а) в форме круга;
б) в форме кольца.
5. Сравнить массы получившихся брусьев, через отношение площадей поперечных сечений:

Пример 4 Для заданного бруса подобрать размеры сечения в двух вариантах: а) круг; б) кольцо, с заданным соотношением  внутреннего и наружного диаметров. Сравнить массы брусьев по обоим расчетным вариантам. Для материала бруса (сталь СтЗ) принять допускаемое напряжение при кручении
внутреннего и наружного диаметров. Сравнить массы брусьев по обоим расчетным вариантам. Для материала бруса (сталь СтЗ) принять допускаемое напряжение при кручении  . Рисунок 12.
. Рисунок 12.
m1=0,9kH·м m2=1,5kH·м
 |
 1уч. 2уч.
1уч. 2уч.
Эпюра «Мк», kН·м















 0,9
0,9
 | |||
 |
0,6
Рисунок 12
Решение:
1. Разбиваем брус на участки по сечениям, в которых приложены скручивающие моменты  и
и  . В заданном брусе два участка.
. В заданном брусе два участка.
2. Пользуясь методом сечений определяем внутренние крутящие моменты  на каждом участке, выбрав правило знаков (знак крутящего момента физического смысла не имеет).
на каждом участке, выбрав правило знаков (знак крутящего момента физического смысла не имеет).
1 участок: 
2участок: 
Построим эпюру крутящих моментов, рисунок 12. Построение эпюры крутящих моментов аналогично построению эпюры продольных сил.
3. Определим размеры поперечного сечения бруса. Для этого используем условие прочности при кручении:

где  - максимальный по модулю крутящий момент, выбирается по эпюре крутящих моментов. Выбираем
- максимальный по модулю крутящий момент, выбирается по эпюре крутящих моментов. Выбираем 
 - допускаемое напряжение при кручении, из условия задачи
- допускаемое напряжение при кручении, из условия задачи 
 - полярный момент сопротивления.
- полярный момент сопротивления.
а) определяем диаметр бруса, если в сечении круг. Полярный момент сопротивления для круга определяется по формуле:

Подставим значение  в формулу условия прочности:
в формулу условия прочности:

Выразим из формулы диаметр d:

Округлим полученный результат до целого числа в большую сторону. Принимаем диаметр бруса  .
.
б) определяем внутренний и наружный диаметры бруса, если в сечении кольцо, с заданным соотношением диаметров  . Полярный момент сопротивления для кольца определяется по формуле:
. Полярный момент сопротивления для кольца определяется по формуле:
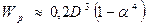 .
.
Подставим значение  в формулу условия прочности:
в формулу условия прочности:

Выразим из формулы диаметр D:

Принимаем D = 44мм. Тогда:
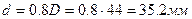
Принимаем d = 35 мм
4. Сравним массы брусьев пообоим расчетным вариантам. Отношение масс брусьев одинаковой длины равно отношению площадей их сечений.
Площадь круглого сечения:

Площадь кольцевого сечения:

Тогда:

Следовательно, брус круглого сечения, выдерживающий заданную нагрузку тяжелее бруса кольцевого сечения в 1,93 раза.
|
|
Дата добавления: 2017-01-14; Просмотров: 774; Нарушение авторских прав?; Мы поможем в написании вашей работы!