Последовательный колебательный контур.

Лекция 3.

Лекция 2.

КУРС ЛЕКЦИЙ

Лекции по дисциплине "Электрорадиотехника"

(9 семестр)

Лекция 1.

Тема: Исторические сведения о развитии электроники. Элементы электрических цепей: резистор, катушка индуктивности, конденсатор, трансформатор, источник напряжения, источник тока. Схемы замещения. Линейные и нелинейные элементы, соотношения между токами и напряжениями для них. Принцип суперпозиции для линейных цепей. Электрическая цепь как устройство для передачи и преобразования энергии и информации. Прохождение токов различной формы через электрические цепи.

Импульсные сигналы и их параметры. Переходные процессы в цепях с резистором, конденсатором и катушкой индуктивности. Простейшие четырехполюсники и их АЧХ и ФЧХ. Коэффициент передачи. Полоса пропускания. Граничные частоты.

Цепь является линейной, если линейны составляющие ее элементы. Элемент, подчиняющийся закону Ома, называют линейным. В природе нет жестких границ. Один и тот же элемент в одних условиях проявляет себя как линейный, в других – как нелинейный. Например, при большой силе тока происходит нагревание проводника, сопровождающееся увеличением его сопротивления. Следовательно, сопротивление проводника начинает зависеть от протекающего тока; в этих условиях он перестает подчиняться закону Ома, т.е. становиться нелинейным.

Индуктивность катушки с ферромагнитным сердечником по мере увеличения силы тока сначала постоянна, а затем также начинает зависеть от неё. Область значения силы тока, в которой индуктивность становится нелинейной, соответствует той части кривой намагничивания B(H), где магнитная проницаемость сердечника начинает зависеть от тока (рис.1.).

Когда сила тока в элементах радиотехнической цепи относительно невелика, зависимости сопротивления и индуктивности от протекающего тока не проявляется; эти элементы, а также конденсаторы являются линейными.

Типичными нелинейными элементами, часто используемыми в радиотехнических цепях и устройствах, являются электронные приборы (электронные лампы, полупроводниковые диоды, транзисторы). Однако и они могут работать в таком режиме, что их нелинейность для переменных составляющих напряжения и тока не проявляется.

Электрические свойства линейной радиотехнической цепи определяются индуктивностью L, емкостью C и сопротивлением R. Если эти параметры не зависят от времени, радиотехническую цепь называют цепью с постоянными параметрами.

Наряду с такими цепями важную роль в радиотехнике играют цепи, параметры которых являются функциями времени. Цепь зависящими от времени параметрами называют параметрической.

Любой элемент проводника обладает некоторой индуктивностью, сопротивлением и ёмкостью относительно других проводников

Рис.1.

Так, реальная катушка обла­дает не только индуктивностью, но также активным сопротивлени­ем и межвитковой емкостью. Твер­дые диэлектрики конденсаторов не являются идеальными, поэтому любой конденсатор характеризу­ется не только емкостью, но и ак­тивной проводимостью. Провод­ники, соединяющие отдельные элементы между собой, также ха­рактеризуются некоторыми пара­метрами L, R, С, распределен­ными по их длине.

Таким образом, в общем слу­чае в реальной системе имеются как сосредоточенные, так и распределенные по ее длине параметры L, R,С. Замена реальной системы системой с сосредоточенными параметрами является некоторым приближением к действительности, значи­тельно упрощающим анализ физических процессов в системе и их математическое описание. Чтобы понять, при каких усло­виях можно не учитывать распределенные параметры, т. е. за­менять реальную систему идеализированной моделью с сосре­доточенными параметрами, надо принять во внимание, что пе­редача сигнала по системе осуществляется электромагнитным полем, существующим в окружающем пространстве. Система с сосредоточенными параметрами является хорошей моделью реаль­ной системы в том случае, когда ее линейные размеры I много меньше длины электромагнитной волны , возбуждаемой системой в окружающем пространстве ( намного меньше ). Если период электромагнитных колебаний в системе Т и скорость электромагнитных волн с, то

=сТ, и условие намного меньше означает, что . Величина — это время, за которое электромагнитная волна проходит расстояние, равное линейному размеру системы. Поскольку передача электри­ческих сигналов в радиотехнической системе происходит со скоростью с, малость по сравнению с периодом Т означает, что сигнал, поступивший на вход системы, практически мгновенно через нее проходит. Отсюда, в частности, следует, что в системе, пред­ставляющей собой цепь последовательно соединенных элементов, сила тока в данный момент времени будет одинаковой во всех элементах цепи. Ситуация аналогична той, которая наблюдается в последовательной цепи постоянного тока. В соответствии с этим системы с сосредоточенными параметрами называют квазистацио­нарными. Напряжения на различных участках квазистационарной системы и силы тока в них зависят только от времени и не зависят от координат, поэтому в уравнениях, описывающих эти системы, фигурируют полные производные по времени.

В ряде случаев L-, R-, С-параметры системы принципиально нельзя считать сосредоточенными, так как они равномерно рас­пределены по всей длине системы (примером таких систем являются длинные линии и антенны). Размеры систем с распределенными параметрами сравнимы с длиной волны, поэтому силы тока в них и напряжения зависят не только от времени, но и от координат. За­висимость от координаты появляется из-за того, что при больших линейных размерах системы необходимо учитывать время распро­странения сигнала от входа до рассматриваемой точки системы. Пусть, например, вдоль оси х линейный размер системы сопоставим с длиной волны. Тогда время, в течение которого электрический сигнал, поступивший на вход системы, достигнет сечения с коорди­натой х, будет сравнимо с периодом колебаний и этим временем нельзя пренебречь. Значит, сила тока в сечении х и напряжение в момент времени t будут определяться значением напряжения вход­ного сигнала не в момент времени t, а в предшествующий момент времени Радиотехническую систему, в которой токии напряжения зависят не только от времени, но и от координаты, называют волновой.

Линейные системы описываются линейными алгебраическими или дифференциальными уравнениями в полных производных по времени в случае квазистационарных систем или в частных производных по времени и координате в случае волновых систем. Параметрические системы описываются линейными дифференциальными уравнениями с переменными (т. е. зависящими от времени) коэффициентами. Теория этих уравнений более сложная по сравнению с теорией ли­нейных уравнений с постоянными коэффициентами, поэтому коли­чественное исследование параметрических систем представляет собой достаточно трудную задачу.

Важным свойством линейных систем как с постоянными, так и с переменными параметрами является справедливость для них принципа суперпозиции, суть которого состоит в следующем. Электрический сигнал (например, напряжение), поступающий на вход радиотехнической системы, назовем воздействием, а сигнал (напряжение или ток), появляющийся на ее выходе,— откликом. Если система линейная, то при наличии одновременно нескольких воздействий отклики систем на каждое из них независимы друг от друга. Это означает, что отклик линейной системы на внешнее воздействие, являющееся суммой нескольких воздействий, может быть получен как сумма (суперпозиция) откликов на каждое из воздействий в отдельности. С математической точки зрения, выпол­нимость принципа суперпозиции обусловлена линейностью диффе­ренциальных уравнений, описывающих систему. Принцип супер­позиции значительно упрощает теоретическое исследование ли­нейных систем при сложном внешнем воздействии. При этом слож­ное воздействие, разлагается на более простые, для которых на­хождение отклика системы не составляет труда. В радиотехнике для разложения сложного воздействия на более простые обычно пользуются рядом (или интегралом) Фурье, т. е. представляют сложное воздействие в виде суммы гармонических воздействий. Отклик линейной системы с постоянными параметрами на гармо­ническое воздействие частоты также является гармоническим с той же частотой. Если на вход линейной системы с постоянными параметрами воздействует напряжение, являющееся суммой нескольких гармонических напряжений, то отклик также можно представить суммой гармонических откликов тех же частот. Это означает, что в спектре отклика линейной системы с постоянными параметрами не могут появиться частоты, отсутствующие в спектре входного воздействия, т. е. в этой системе не возникают новые частоты.

Принцип суперпозиции применим, как уже отмечалось, и к ли­нейной системе с переменными параметрами. Однако в этом слу­чае в спектре отклика появляются новые частоты, что можно ил­люстрировать следующим примером. Рассмотрим простейшую цепь, состоящую из двух последовательно соединенных активных сопро­тивлений (рис. 2.2), одно из которых R_o постоянно, другое меняется со временем около некоторого среднего значения R₁по гармони­ческому закону: 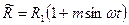, где .

Пусть входное напряжение (воздействие) с частотой является гармонической функцией времени: .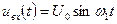

В соответствии с рисунком 2.2, входное напряжение (отклик) , где - сила тока в цепи. Подставив значения и для , получим:

(1.1)

Где .

Преобразуем (1.1) в предположении, что :

. (1.2)

Из (1.2) видно, что, кроме гармонической составляющей с частотой , равной частоте входного воздействия, в выходном напряжении имеются гармонический составляющие с частотами . В общем случае, когда не делается предположения о малости отношения 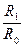по сравнению с единицей, в спектре выходного напряжения кроме частоты будут представлены все частоты вида 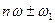, где n принимает целочисленные значения от 1 до . Взяв входное воздействие в виде суммы нескольких гармонических напряжений, нетрудно убедиться в справедливости принципа суперпозиции для параметрической системы, изображенной на рис 2.

Рис. 2.

Тема: Полевые (p-n переходом и изолированным затвором) и биполярные транзисторы. Принцип работы, статические ВАХ, параметры, простейшие эквивалентные схемы. Режим работы (активный, отсечки, насыщения).

Полевой транзистор – полупроводниковый прибор, в котором выходной ток управляется входным напряжением. Транзистор называется полевым, так как входное напряжение создает электрическое поле, влияющее на выходной ток. Благодаря управлению электрическим полем входное сопротивление полевых транзисторов для постоянного тока и низкой частоты переменного тока может быть очень больши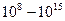м: Ом.

В биполярных транзисторах существенную роль играют два типа носителей электрического тока: основные и не основные. В полевых транзисторах ток создается основным типом носителей. Поэтому иногда полевые транзисторы называют униполярными.

Полевые транзисторы подразделяются на полевые транзисторы с управляющим р-n переходом и с изолированным затвором. Полевые транзисторы с изолированным затвором в свою очередь подразделяются на транзисторы со встроенным каналом и транзисторы с индуцированным каналом. Канал в полевых транзисторах может быть n или p типа.

Канал - это область полевого транзистора, через которую протекают основные носители заряда. Величина тока в канале управляется электрическим полем. Транзисторы имеют 3 вывода. Вывод, от которого в канал приходят основные носители заряда, называется истоком. Вывод, к которому носители заряда приходят из канала, называется стоком. Вывод, на который подается управляющее напряжение относительно истока или стока, называется затвором.

Ток в полевом транзисторе течет от истока к стоку. Если канал n-типа, то к стоку двигаются электроны; если канал p-типа, то к стоку двигаются дырки.

Для того чтобы определить тип канала и выводы транзистора, можно воспользоваться омметром. Величина сопротивления между предполагаемыми выводами истока и стока не зависит от полярности подключения щупов омметра. Величина сопротивления между затвором и истоком (стоком) зависит от полярности подключения щупов омметра. Таким образом, мы выясняем, какой из выводов является выводом затвора. Если при малом сопротивлении перехода з-и транзистора плюсовой щуп омметра касался вывода затвора, то затвор р-типа, а канал n-типа. В противном случае - канал р-типа.

Стоковая характеристика полевого транзистора для схемы включения транзистора с общим истоком – это зависимость тока стока от напряжения сток-исток при постоянном напряжении затвор-исток.

Тема: Последовательный и параллельный колебательные контуры. Резонанс токов и напряжений. Влияние внутреннего сопротивления источника и сопротивления нагрузки на резонансные свойства колебательных контуров.

Последовательный колебательный контур можно представить в виде четырехполюсника.

	b′

Рис.3

b

На рис.3 емкостное сопротивление Х_с подключено к клеммам а^′ и b′. Такое представление колебательного контура в виде четырехполюсника не единственное. К клеммам а^′ и b′ может быть подключена и катушка индуктивности. Отметим, что активное сопротивление К включает в себя активное сопротивление катушки и активное сопротивление конденсатора:

Известно, что полное сопротивление последовательного колебательного контура может быть представлено комплексным числом:

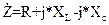(1),

,

.

Выражение (1) можно представить в показательной форме комплексного числа:

,

где , ,

Z – это модуль комплексного числа ,

- аргумент комплексного числа .

X

Из треугольника сопротивлений можно выразить через активное и реактивное сопротивление. (2).

При определенном значении частоты, реактивные сопротивления могут быть равны друг другу:

(3) – условие резонанса,

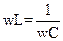(3′).

При w=w₀ может быть выполнено равенство (3′).

,

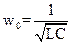- резонансная частота колебательного контура.

(4)

(4) - характеристическое сопротивление (волновое сопротивление).

Отношение волнового сопротивления к активному сопротивлению называется добротностью колебательного контура.

(5)

В радиотехнике полное сопротивление электрической цепи принято называть импедансом.

Построим графики зависимостей реактивных сопротивлений от частоты.

X_C(w)

, X=0.

Подключим колебательный контур к источнику синусоидального напряжения.

,

- начальная фаза колебаний.

Для простоты рассмотрим пример: t=0

В электрической цепи потечет ток, величина которого будет определяться по формуле:

(6).

При резонансе, когда , полное сопротивление колебательного контура (импеданс колебательного контура) Z=R.

.

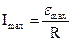X=X_L- X_C=0, а , (*)

Выражение (*) говорит о том, что колебания тока совпадают с колебаниями ЭДС при резонансе.

Дата добавления: 2017-02-01