
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Число уравнений и неизвестных равно 3
|
|
|
|
Рассмотрим СЛУ
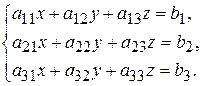
Вычисляются определители:
 ,
,  ,
,
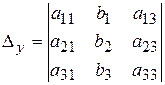 ,
,  .
.
1. Если  , то система имеет единственное решение, которое находится по формулам Крамера:
, то система имеет единственное решение, которое находится по формулам Крамера:

 ,
,  .
.
2. Если  , а хотя бы один из определителей
, а хотя бы один из определителей  ,
,  ,
,  отличен от нуля, то система не имеет решений.
отличен от нуля, то система не имеет решений.
3. Если 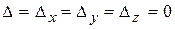 , то система имеет бесконечно много решений.
, то система имеет бесконечно много решений.
Пример 4. Решить систему линейных уравнений  .
.
Составим определитель из коэффициентов при неизвестных и вычислим его:  ,
,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители и значения неизвестных.




Ответ: Система совместная и определенная, единственное решение  .
.
Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера.
Пример 5. Решить СЛУ 
Решение
Вычислим определитель системы: 
Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений.
Отбросив третье уравнение, получим равносильную систему двух уравнений с тремя неизвестными: 
Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю.
Например, коэффициенты при  и
и  образуют определитель
образуют определитель  . Поэтому оставим в левой части уравнений слагаемые с
. Поэтому оставим в левой части уравнений слагаемые с  и
и  , а слагаемые с
, а слагаемые с  перенесем в правую часть с противоположным знаком.
перенесем в правую часть с противоположным знаком.
Неизвестное  назовем свободным, а неизвестные
назовем свободным, а неизвестные  и
и  - базисными неизвестными.
- базисными неизвестными.
Запишем систему в виде 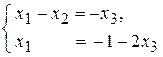 и применим к ней правило Крамера:
и применим к ней правило Крамера:
 ;
;

Выражение
 -
-
общее решениенеопределенной СЛУ, где  - любое действительное число.
- любое действительное число.
Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение.
Например, пусть 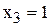 , тогда
, тогда  ; тогда частное решение
; тогда частное решение  . И так далее.
. И так далее.
| 4. Ранг матрицы. Теорема Кронекера-Капелли |
Определение 1. Пусть имеется матрица размерности  : :
 .
Минором k-го порядка данной матрицы называется определитель, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы.
Пример. В матрице .
Минором k-го порядка данной матрицы называется определитель, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы.
Пример. В матрице 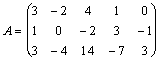 минорами первого порядка являются сами элементы матрицы. Если выбрать две строчки (например, 1-ю и 3-ю) и два столбца (например, 2-й и 5-й), получится минор второго порядка минорами первого порядка являются сами элементы матрицы. Если выбрать две строчки (например, 1-ю и 3-ю) и два столбца (например, 2-й и 5-й), получится минор второго порядка  . Если взять три строки и три столбца (например, 1-й, 3-й, и 4-й), получится минор 3-го порядка . Если взять три строки и три столбца (например, 1-й, 3-й, и 4-й), получится минор 3-го порядка
 .
Определение 2. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.
Пример. В рассмотренной выше матрице .
Определение 2. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.
Пример. В рассмотренной выше матрице  все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы  равен двум. Это обозначается: равен двум. Это обозначается:  .
Определение 3. Две матрицы .
Определение 3. Две матрицы 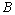 и и  называются эквивалентными (пишут: называются эквивалентными (пишут:  ), если их ранги равны: ), если их ранги равны:  .
Можно показать, что следующие преобразования не меняют ранга матрицы:
1) перестановка строк матрицы;
2) умножение какой-либо строки на действительное число, отличное от нуля;
3) прибавление к элементам одной строки соответствующих элементов другой строки;
4) вычеркивание строки, все элементы которой равны нулю.
Указанные преобразования можно использовать для определения ранга матрицы.
Пример. Для определения ранга матрицы .
Можно показать, что следующие преобразования не меняют ранга матрицы:
1) перестановка строк матрицы;
2) умножение какой-либо строки на действительное число, отличное от нуля;
3) прибавление к элементам одной строки соответствующих элементов другой строки;
4) вычеркивание строки, все элементы которой равны нулю.
Указанные преобразования можно использовать для определения ранга матрицы.
Пример. Для определения ранга матрицы  необходимо выполнить цепочку следующих преобразований: необходимо выполнить цепочку следующих преобразований:
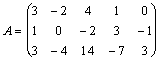 ~ ~  (переставили местами первую и вторую строки) ~ (переставили местами первую и вторую строки) ~  (первую строку умножили на (первую строку умножили на  и сложили со второй; первую строку умножили на и сложили со второй; первую строку умножили на  и сложили с третьей) ~ и сложили с третьей) ~  (элементы третьей строки умножили на (элементы третьей строки умножили на
 ) ~ ) ~  (к элементам третьей строки прибавили элементы второй строки). Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы (к элементам третьей строки прибавили элементы второй строки). Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы  равен двум: равен двум:  .
Определение 4. Пусть дана система .
Определение 4. Пусть дана система  линейных уравнений с линейных уравнений с  неизвестными: неизвестными:
 Матрицей системы называют матрицу, составленную из коэффициентов при неизвестных, расширенной матрицей системы – матрицу из коэффициентов с дополнительным столбцом из свободных членов. Если обозначить их соответственно
Матрицей системы называют матрицу, составленную из коэффициентов при неизвестных, расширенной матрицей системы – матрицу из коэффициентов с дополнительным столбцом из свободных членов. Если обозначить их соответственно  и и  , то , то
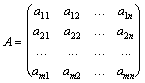 , , 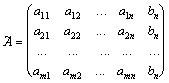 .
Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.
Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество.
Пример. Исследовать систему линейных уравнений .
Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.
Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество.
Пример. Исследовать систему линейных уравнений
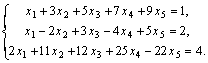 Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно.
Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно.
  ~ ~  ~
~ ~
~  .
Таким образом, матрица .
Таким образом, матрица  содержит две ненулевые строки, значит ее ранг содержит две ненулевые строки, значит ее ранг  равен двум. В матрице равен двум. В матрице 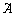 три ненулевых строки, ее ранг три ненулевых строки, ее ранг  равен трем. А т.к. равен трем. А т.к.  , система несовместна. , система несовместна.
|
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 65; Нарушение авторских прав?; Мы поможем в написании вашей работы!