Последовательность выполнения работы

Вычислительные методы

Статистические параметры распределения могут быть вычислены по тем формулам, по которым они определяются. Однако существует способ вычислений, позволяющий избежать вычисления отклонений d_i –` d и, тем самым, сократить общее число арифметических действий и промежуточных округлений. Когда проводится полная статистическая обработка большого объема данных, применяют именно его. Этот способ называется методом начальных моментов.

Начальным моментом k -ого порядка (или k -ым начальным моментом распределения) называется величина:

(11)

То есть, , , ,....

Преобразованием формул (5), (6), (7), (10) можно найти:

` d = n₁ (12)

s ² = n₂ 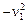(13)

(14)

Исходными в этой работе считаются данные о числах N_i наблюдений диаметра частиц в интервалах диаметра D d. Общая схема выполнения работы следующая.

I) Из исходных данных вычисляются диаметры d_i в серединах интервалов (карманов) и частоты f_i. По ним строится гистограмма, и из неё (или из таблицы) определяется мода распределения.

II) Вычисляется кумулятивная частота F_i. По этим данным строится диаграмма кумулятивного распределения. Из неё (или из таблицы) определяется медиана распределения.

III) Вычисляется первый начальный момент n₁ и, таким образом, средний арифметический диаметр` d.

IV) Вычисляется второй начальный момент n₂ и, с его помощью, дисперсия s ², среднее квадратичное отклонение s, и коэффициент вариации V.

V) Вычисляется третий начальный момент n₃ и, с его помощью, коэффициент асимметрии А.

Более подробно последовательность анализа данных объясняется ниже на примере статистики в табл. 1.

1. Вычисляются диаметры d_i в серединах интервалов D d, как полусумма нижней границы интервала i +1 и нижней границы интервала i. Например, диаметр d в первой строке в колонке 2 равен (6 + 4)/2 = 5. Аналогично в остальных строках, кроме последней, где d равен полусумме верхней и нижней границ интервала, d = (28 + 26)/2 = 27. Результаты занесены в колонку 2.

2. Вычисляется общее число измерений N как сумма всех N_i в колонке 3. Найденная величина N = 1730 указана внизу колонки 3.

3. Вычисляются частоты f_i наблюдений диаметров d_i делением каждого N_i на N. Результаты заносятся в колонку 4.

4. По результатам в колонках 4 и 2 строится гистограмма (рис. 2А).

5. Из гистограммы (или из таблицы) определяется мода или моды распределения. В частности, из рис. 2А видно, что распределение имеет один максимум, приходящийся на d = 15 нм. То есть, распределение имеет моду М = 15 нм.

6. В колонке 5 вычисляется кумулятивная частота F_i. В каждой строке i она равна сумме частоты f_i в той же строке i (колонка 4) и накопленной частоты в предыдущей строке i –1: F_i = f_i + F_{i –1}. Например, во второй строке F ₂ = f ₂ + F ₁ = 0.0315 + 0.0035 = 0.0350. Аналогично в остальных строках, но в первой строке F ₁ = f ₁ + 0 = f ₁ = 0.0035.

7. По результатам в колонках 5 и 2 строится диаграмма кумулятивного распределения (рис. 2Б).

8. Из полученной диаграммы (или из таблицы) определяется медиана распределения. В частности, из рис. 2Б видно, что величина F = 0.5 приходится между столбцами диаграммы при d = 13 нм и d = 15 нм. Поэтому распределение имеет медиану m = 14 нм.

9. В колонке 6, в каждой строке i, вычисляется произведение частоты и диаметра f_id_i.

10. Вычисляется первый начальный момент по формуле (11) как сумма произведений f_id_i по всем строкам колонки 6. Результат n₁ = 15.1781 нм указан внизу колонки.

11. В соответствии с формулой (12), получается среднее арифметическое,` d = n₁ = 15.2 нм.

12. В колонке 7, в каждой строке i, вычисляется произведение умножением произведения f_id_i в той же строке (колонка 6) и диаметра d_i в той же строке (колонка 2), = f_id_i × d_i.

13. Вычисляется второй начальный момент по формуле (11) как сумма произведений по всем строкам колонки 7. Результат n₂ = 247.427 нм² указан внизу колонки.

14. По формуле (13) получается дисперсия s ² = n₂ 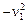= 247.427 нм² – (15.1781 нм)² = 17.1 нм², а из неё по формуле (7) получается среднее квадратичное отклонение s = = 4.1 нм.

15. По формуле (8) вычисляется коэффициент вариации = (4.1 нм)/(15.2 нм) = 0.27 = 27 %.

16. В колонке 8, в каждой строке i, вычисляется произведение умножением произведения в той же строке (колонка 7) и диаметра d_i в той же строке (колонка 2), = × d_i.

17. Вычисляется третий начальный момент по формуле (11) как сумма произведений по всем строкам колонки 8. Результат n₃ = 4298.04 нм³ указан внизу колонки.

18. По формуле (14) вычисляется показатель асимметрии:

= [4298.04 нм³ – 3(247.427 нм²)(15.1781 нм) + 2(15.1781 нм)³]/(4.1 нм)³ = 0.35.

Выводы: ` d = 15.2 нм, s = 4.1 нм, коэффициент вариации 27 %, мода 15 нм, медиана 14 нм, коэффициент асимметрии 0.35.

Задание

Для своего варианта статистических данных измерения диаметра проекционной площади наночастиц построить гистограмму и диаграмму кумулятивного распределения, вычислить средний арифметический диаметр, среднее квадратичное отклонение, коэффициент вариации, показатель асимметрии, а также определить моду и медиану распределения.

Контрольные вопросы

1. Какое свойство распределения характеризует среднее арифметическое?

2. Какое свойство распределения характеризует показатель асимметрии?

3. Какое свойство распределения характеризует мода?

4. Какое свойство распределения характеризует среднее квадратичное отклонение?

5. Какое свойство теоретического распределения характеризует стандартное отклонение?

6. Какое свойство распределения характеризует медиана?

7. Почему наряду со средним квадратичным отклонением применяется коэффициент вариации?

8. Зачем наряду со многими другими статистическими характеристиками вычисляют также начальные моменты распределения?

Вариант 2  

D d /нм	Ni
1.33–1.99
2.00–2.66
2.67–3.32
3.33–3.99
4.00–4.66
4.67–5.32
5.33–5.99
6.00–6.66
6.67–7.32
7.33–7.99
8.00–8.66
8.67–9.32
9.33–9.99
10.00–10.66
10.67–11.32
11.33–11.99
12.00–12.66
12.67–13.32
13.33–14.00

Вариант 3  

D d /нм	Ni
3.33–6.66
6.67–9.99
10.00–12.32
13.33–16.66
16.67–19.99
20.00–23.32
23.33–26.66
26.67–29.99
30.00–33.32
33.33–36.66
36.67–39.99
40.00–43.32
43.33–46.66
46.67–49.99
50.00–53.32
53.33–56.66
56.67–60.00

Вариант 5  

D d /нм	Ni
50–99
100–149
150–199
200–249
250–299
300–349
350–399
400–449
450–499
500–549
550–600

Вариант 6  

D d /мкм	Ni
0–0.09
0.10–0.19
0.20–0.29
0.30–0.39
0.40–0.49
0.50–0.59
0.60–0.69
0.70–0.79
0.80–0.89
0.90–0.99
1.00–1.09
1.10–1.20

Литература.

1. Hunter R.J. Foundations of colloid science. 2nd ed. Oxford: Oxford

University Press, 2001

2. Barlow R.J. Statistics: a guide to the use of statistical methods

in the physical sciences. Chichester: Wiley, 1989

3. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и

математической статистики для технических приложений. 3-е изд. Москва:

Наука, 1969

ЛАБОРАТОРНАЯ РАБОТА № 2

Дата добавления: 2017-02-01