Тема 3 Целочисленное программирование 1 страница

Введение

Тестирование решения

Получить у преподавателя номер варианта.

Запустить Snort cо следующими параметрами:

snort -c /etc/snort/snort.conf -r [filename].cap.

Посмотреть наличие/отсутствие зафиксированных событий безопасности при правилах СОА Snort активных по-умолчанию.

Сделать активными все правила СОА Snort и повторить исследование файла с трафиком. Указать:

- общее количество зафиксированных событий безопасности;

- количество зафиксированных уникальных событий безопасности.

Для каждого из уникальных событий указать:

- общее количество;

- количество уникальных адресов источника и назначения;

- время первого и последнего события безопасности;

- на использование какой уязвимости направлена зафиксированная попытка вторжения.

Задание 2.

По результатам выполненной работы представить отчет преподавателю в письменном виде. Данные по результатам выполнения задания № 1 оформить в табличном виде. Дать рекомендации по устранению выявленных путем анализа сетевого трафика угроз безопасности.

Машины лабораторного стенда оставить для проверки в конечном виде.

Задание 3.

Написать правила для СОА Snort для генерации событий безопасности в соотвествии с требованиями, выданными преподавателем.

Методы экономико-математического моделирования представляют собой один из наиболее динамично развивающихся разделов прикладной науки. Дисциплина занимает важное место в системе подготовки специалистов и входит в блок дисциплин, обязательных для изучения.

Специалисты должны уметь использовать методы сбора и обработки статистической информации, оценки состояния и перспективы развития процессов. При этом применяются различные способы использования полученной информации – от простого логического анализа до составления сложных экономико-математических моделей и разработки математического аппарата их исследования.

Основы математического моделирования широко применяются в приложениях, в базовых учебных дисциплинах при подготовке специалистов и являются переходом к теоретическому обоснованию прикладной роли математики в подготовке специалистов.

Изучение многих вопросов предполагает наличие у студентов достаточно высокого уровня математической подготовки по основам высшей математики, математическому анализу, так как неопределенность экономических процессов, значительный случайный разброс и большой объем получаемой информации обуславливают необходимость привлечения к исследованию экономических задач теории вероятностей и математической статистики.

Наряду с моделированием студентам необходимо изучать теорию оптимизации, которая представлена математическими методами исследования операций, в том числе линейным программированием.

Практикум предназначен для формирования устойчивых навыков решения задач по дисциплине «Экономические методы и моделирование».

Содержание

Практикум содержит:

· Образцы решения типовых задач по темам;

· Задания для самостоятельной работы студентов, предназначенные для получения баллов при определении рейтинга успеваемости студента;

· Список основной и дополнительной литературы по дисциплине.

Данная структура позволяет студентам в условиях минимизации учебного времени необходимо получить максимальный образовательный эффект, сокращает потери времени на решение организационных задач и на поиск необходимой информации и позволяет эффективно использовать учебное время для решения задач и усвоения необходимого материала.

Тема 1. Графическое решение задач линейного программирования

Математическое программирование – раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций (целевых функций) нескольких переменных при наличии ограничений на эти переменные.

В общем виде задача математического программирования имеет вид:

f(X) → min(max); X є D, (1)

где X = (x₁, x₂,..., x_n) – вектор переменных задачи;

D – область допустимых значений переменных x₁, x₂,..., x_n, задаваемая системой ограничений в виде уравнений и неравенств;

f(X) – целевая функция, характеризующая качество решения задачи.

В математическом программировании в зависимости от вида целевой функции f(X) и области D принято выделять следующие основные задачи:

-задачи линейного программирования, если f(X) и D линейны по X;

-задачи дискретного (целочисленного) программирования, если ставится условие целочисленности переменных x₁, x₂,..., x_n;

-задачи нелинейного программирования, если f(X) и D нелинейны по X;

-задачи динамического программирования, если оптимизация целевой функции f(X) сводится к поэтапной оптимизации некоторых промежуточных целевых функций.

Основные определения и понятия линейного программирования.

Общая задача линейного программирования (ОЗЛП) формулируется следующим образом – найти переменные задачи x₁, x₂,..., x_n, которые обеспечивают экстремум целевой функции

…………. (1.1)

Допустимым решением (планом) задачи линейного программирования (ЗЛП) называется любой n-мерный вектор X=(x₁, x₂,..., x_n), удовлетворяющий системе ограничений равенств и неравенств. Множество допустимых решений задачи образует область допустимых решений D.

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение, при котором целевая функция Z(X) достигает экстремума.

Каноническая задача линейного программирования (КЗЛП) имеет вид

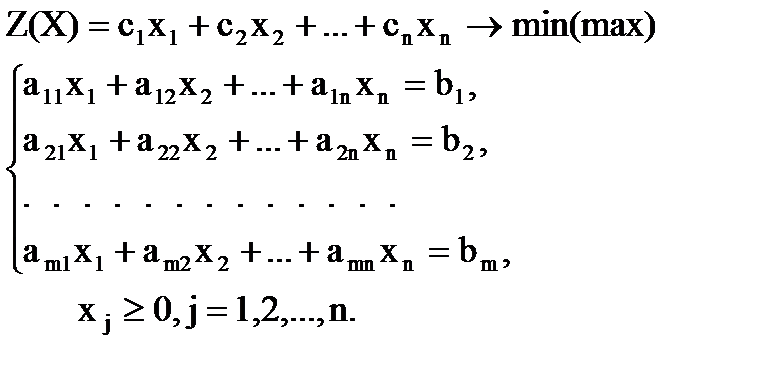(1.2)

Она отличается от ОЗЛП тем, что её система ограничений является системой только уравнений и все переменные неотрицательные.

Приведение ОЗЛП к каноническому виду ЗЛП:

чтобы заменить исходную задачу минимизации на задачу максимизации (или наоборот задачу максимизации на задачу минимизации) достаточно целевую функцию умножить на «-1» и искать максимум (минимум) полученной функции;

если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных x_n+1 ≥ 0 они преобразуются в равенства:

неравенство a_i1x₁+…+a_in x_n ≥ b_i заменяется на равенство a_i1x₁+…+a_in x_n + x_n+1 = b_i,

неравенство a_i1x₁+…+a_in x_n ≤ b_i заменяется на равенство a_i1x₁+…+a_in x_n + x_n+1 = b_i;

если некоторая переменная x_k не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательны-ми переменными: x_k = x'_k – x”_k, где x'_k ≥ 0. x”_k ≥ 0.

Графический метод решения ЗЛП с двумя неизвестными

ЗЛП с двумя неизвестными имеет вид:

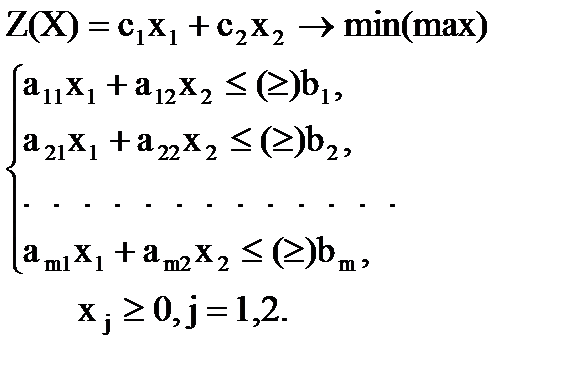
Метод основан на возможности графического изображения области допустимых решений и нахождении среди них оптимального решения.

Область допустимых решений (ОДР) задачи является выпуклым многоугольником и строится как пересечение (общая часть) областей решений каждого из неравенств ограничений задачи.

Областью решения неравенства a_i1x₁+a_i2 x₂ ≤ b_i является одна из двух полуплоскостей, на которые прямая a_i1x₁+a_i2 x₂ = b_i, соответствующая этому неравенству, делит координатную плоскость. Чтобы определить какая из двух полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на разделяющей прямой подставить в неравенство:

- если неравенство справедливо, то областью решений является полуплоскость, содержащая эту точку;

- если неравенство не справедливо, то областью решений является полуплоскость, не содержащая эту точку.

Для нахождения среди допустимых решений оптимального используются линии уровня.

Линией уровня называется прямая с₁x₁+с₂ x₂ = l, где l=const, на которой целевая функция задачи принимает постоянное значение. Все линии уровня параллельны между собой.

Градиент целевой функции grad Z(X) задает вектор нормали C=(c₁, c₂) линий уровня. Целевая функция на линиях уровня возрастает, если линии уровня перемещать в направлении их нормали, и убывает – в противоположном направлении.

Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с ОДР и по отношению к которой ОДР находится в одной из полуплоскостей. ОДР задачи имеет не более двух опорных прямых.

Оптимальное решение ЗЛП лежит на опорной прямой в угловой точке многоугольника ОДР. ЗЛП имеет единственное решение, если опорная прямая проходит через одну угловую точку ОДР, бесконечное множество решений, если опорная прямая проходит через ребро многоугольника ОДР. ЗЛП не имеет решения, если ОДР является пустым множеством (когда система ограничений несовместна) и если ОДР неограниченна в направлении экстремума (целевая функция неограничена).

Алгоритм графического метода решения ЗЛП с двумя неизвестными:

1. Построить ОДР.

2. Построить вектор нормали C=(c₁, c₂) и линию уровня с₁x₁+с₂ x₂ = 0, проходящую через начало координат и перпендикулярную вектору С.

3. Передвигать линию уровня до опорной прямой в направлении вектора С в задаче на max, или в противоположном направлении – в задаче на min.

4. Если при перемещении линии уровня в направлении экстремума ОДР уходит в бесконечность, то ЗЛП не имеет решения ввиду неограниченности целевой функции.

5. Если ЗЛП имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой. Если экстремум достигается в двух угловых точках, то ЗЛП имеет бесконечное множество решений, принадлежащих ребру ОДР, ограниченному этими угловыми точками. В данном случае вычисляются координаты обеих угловых точек.

6. Вычислить значение целевой функции в точке экстремума.

7. Проверить решение на оптимальность.

Задача 1.

Решить графическим методом следующую задачу:

Из трех видов сырья производят два вида продукции. Нормы расхода сырья на одно изделие, запасы сырья на складе и прибыль от продажи единицы каждого вида изделий представлены в таблице. Определить максимально возможное значение прибыли при существующих ограничениях по расходу сырья и план производства продукции.

Таблица 1

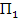
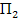
Сырье			Запасы сырья
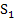
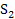
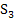
Прибыль П			max

Решение:

Составим математическую модель задачи. Она включает в себя переменные, систему ограничений и целевую функцию.

Пусть 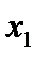-количество продукции вида
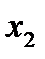-количество продукции вида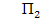

Тогда математическая модель имеет вид

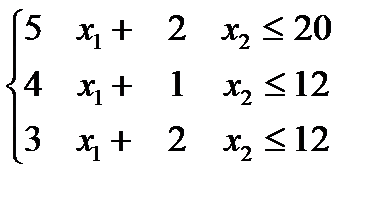
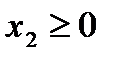
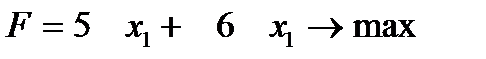Целевая функция

Запишем уравнения графических прямых и построим их в одной системе координат.

Построим граничные прямые

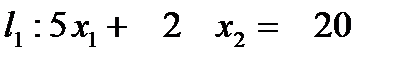
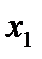
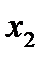
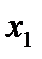
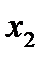
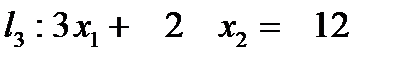
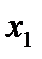
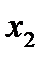
Подставим в исходные неравенства пробную точку и проверим выполнимость неравенств.

Пробная точка

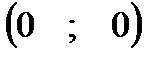
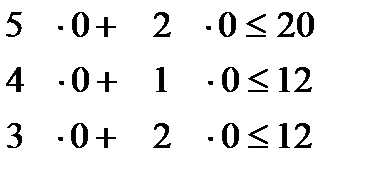
Так как все неравенства верные, то мы можем определить полуплоскости на графике, соответствующие множеству точек- решений для каждого неравенства.

1. Множество допустимых решений задачи образует область допустимых решений (ОДР).

2. Для того, чтобы найти множество точек ОДР, удовлетворяющих заданным неравенствам, нужно:

3. Взять точку с любыми координатами (она называется пробной точкой)

4. Подставить координаты пробной точки в неравенства.

5. Определить полуплоскости, удовлетворяющую данным неравенствам.

6. Если неравенство получается верным, то мы заштриховываем полуплоскость, в которой содержится пробная точка, если неравенство не верное, то штрихуем полуплоскость, в которой пробной точки нет.

7. Заштриховать на чертеже все выбранные полуплоскости и определить область допустимых решений.

Неравенство верное Неравенство не верное

Пробная точка Пробная точка

В данном случае область допустимых значений является выпуклым многоугольником и определяется как общая часть всех заштрихованных областей.

Область допустимых решений (ОДР) задачи является выпуклым многоугольником и строится как пересечение (общая часть) областей решений каждого из неравенств ограничений задачи.

В данном задании это выпуклый четырехугольник ОАВС

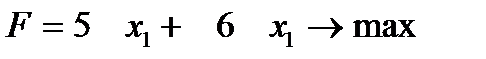
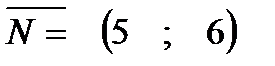Нормальный вектор

Нормальный вектор строится следующим образом: отмечаем точку с координатами (5;6) и соединяем начало координат с данной точкой направленным отрезком.

Градиент целевой функции grad Z(X) это вектор, перпендикулярный линии, изображающей линию задает вектор нормали C=(c₁, c₂) линий уровня.

Целевая функция на линиях уровня возрастает, если линии уровня перемещать в направлении их нормали, и убывает – в противоположном направлении.

• Линией уровня называется прямая с₁x₁+с₂ x_{2 =} l, где l=const, на которой целевая функция задачи принимает постоянное значение. Все линии уровня параллельны между собой.

Построим линии уровня целевой функции.

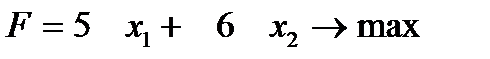целевая функция

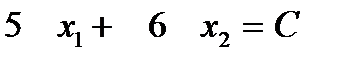Линии уровня целевой функции.

Если С=1, то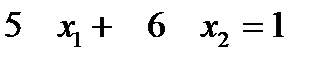

Если С=3, то

Если С=5, то

Если С=8, то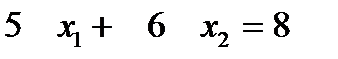

Оптимальное решение ЗЛП лежит на опорной прямой в угловой точке многоугольника ОДР.

Алгоритм графического метода решения ЗЛП с двумя неизвестными:

1. Построим ОДР.

2. Построим вектор нормали C=(c₁, c₂) и линию уровня с₁x₁+с₂ x₂ =0, проходящую через начало координат и перпендикулярную вектору С.

3. Передвинем линию уровня в направлении вектора С

4. Вычислить значение целевой функции в точке экстремума.

Задача 4.

Бригада приняла заказ на изготовление 60.ед продукции вида П1, 30 ед. продукции П2 и 55 ед. продукции П3. продукция производится на станках А и В. Для изготовления на станке А единицы продукции П1 требуется 3 единицы времени, единицы продукции П2 40 ед., единицы продукции П3- 10 ед., на станке В – соответственно 7, 9 и 20 ед. времени. Найти план использования оборудования, чтобы заказ был выполнен в минимальное время.

Решение

Таблица 1

		Станок В
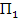
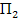
П3
Время			min

	П1	П2	П3
Станок А
Станок В
Продукция

Решение:

Составим математическую модель задачи. Она включает в себя переменные, систему ограничений и целевую функцию.

Пусть

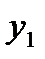-количество продукции изготовлено вида П1

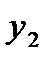-количество продукции изготовлено П2;

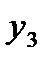-количество продукции изготовлено П3;

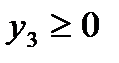
Тогда расход времени

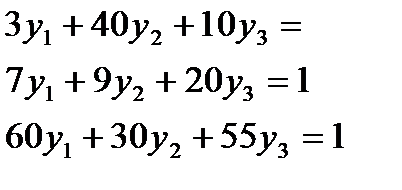
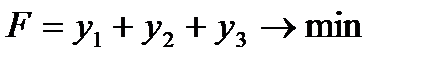Целевая функция

Запишем уравнения графических прямых и построим их в одной системе координат.

Построим граничные прямые

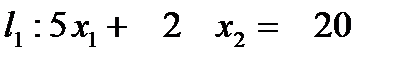
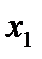
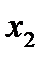
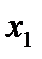
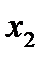
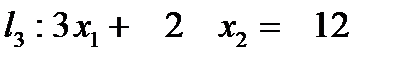
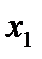
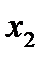
Подставим в исходные неравенства пробную точку и проверим выполнимость неравенств.

Пробная точка

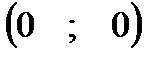
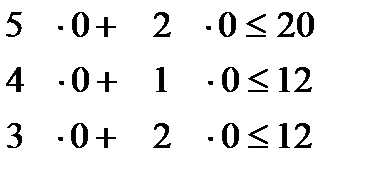
Так как все неравенства верные, то мы можем определить полуплоскости на графике, соответствующие множеству точек- решений для каждого неравенства.

8. Множество допустимых решений задачи образует область допустимых решений (ОДР).

9. Для того, чтобы найти множество точек ОДР, удовлетворяющих заданным неравенствам, нужно:

10. Взять точку с любыми координатами (она называется пробной точкой)

11. Подставить координаты пробной точки в неравенства.

12. Определить полуплоскости, удовлетворяющую данным неравенствам.

13. Если неравенство получается верным, то мы заштриховываем полуплоскость, в которой содержится пробная точка, если неравенство не верное, то штрихуем полуплоскость, в которой пробной точки нет.

14. Заштриховать на чертеже все выбранные полуплоскости и определить область допустимых решений.

Неравенство верное Неравенство не верное

Пробная точка Пробная точка

В данном случае область допустимых значений является выпуклым многоугольником и определяется как общая часть всех заштрихованных областей.

Область допустимых решений (ОДР) задачи является выпуклым многоугольником и строится как пересечение (общая часть) областей решений каждого из неравенств ограничений задачи.

В данном задании это выпуклый четырехугольник ОАВС

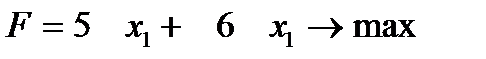
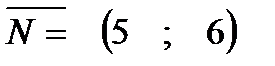Нормальный вектор

Нормальный вектор строится следующим образом: отмечаем точку с координатами (5;6) и соединяем начало координат с данной точкой направленным отрезком.

Градиент целевой функции grad Z(X) это вектор, перпендикулярный линии, изображающей линию задает вектор нормали C=(c₁, c₂) линий уровня.

Целевая функция на линиях уровня возрастает, если линии уровня перемещать в направлении их нормали, и убывает – в противоположном направлении.

• Линией уровня называется прямая с₁x₁+с₂ x_{2 =} l, где l=const, на которой целевая функция задачи принимает постоянное значение. Все линии уровня параллельны между собой.

Построим линии уровня целевой функции.

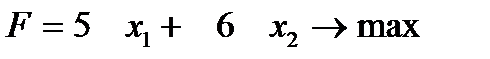целевая функция

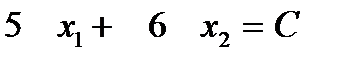Линии уровня целевой функции.

Если С=1, то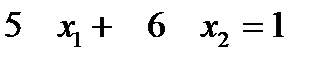

Если С=3, то

Если С=5, то

Если С=8, то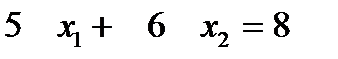

Оптимальное решение ЗЛП лежит на опорной прямой в угловой точке многоугольника ОДР.

Алгоритм графического метода решения ЗЛП с двумя неизвестными:

5. Построим ОДР.

6. Построим вектор нормали C=(c₁, c₂) и линию уровня с₁x₁+с₂ x₂ =0, проходящую через начало координат и перпендикулярную вектору С.

7. Передвинем линию уровня в направлении вектора С

8. Вычислить значение целевой функции в точке экстремума.

Таблица 5 Формы записи задач линейного программирования.

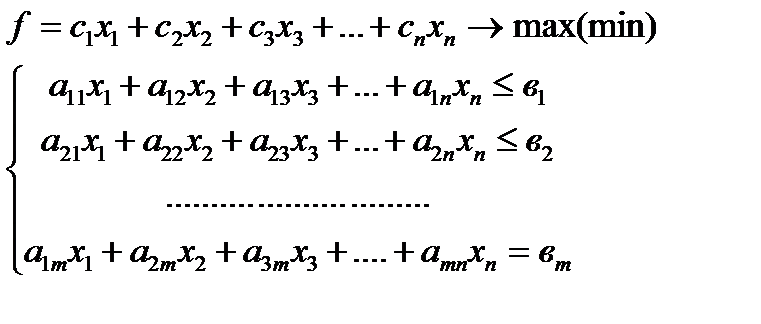
Общая форма	· Целевая функция может стремится как max, так и к min · В системе ограничений содержатся как неравенства, так и уравнения · Не все переменные могут быть неотрицательны
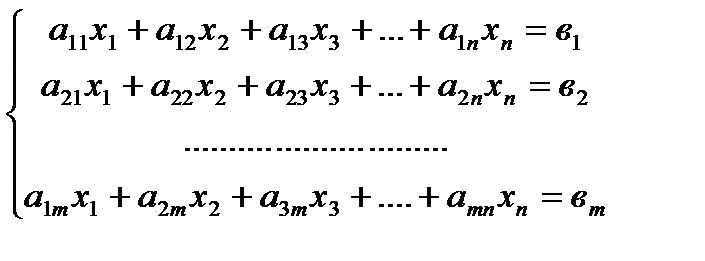
Каноническая форма	· Целевая функция стремится только к max · В системе ограничений содержатся только уравнения · Все переменные неотрицательны
Стандартная форма	· Целевая функция может стремится как max, так и к min · В системе ограничений содержатся только неравенства · Все переменные неотрицательны

Задание 3

Составьте математическую модель задачи:

При производстве двух видов продукции используют три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли.

Таблица 2

Вид сырья	Норма расхода на 1 изделие	Запас на складе
А	Б
прибыль от 1 изделия

Решение:

Пусть 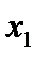-количество продукции вида А

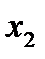-количество продукции вида В

Тогда математическая модель имеет вид

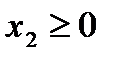
Целевая функция

Задание 4

Решить ЗЛП графическим методом.

Решение:

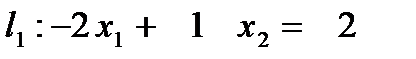
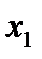
	-1

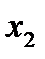
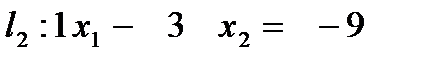
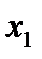
	-9

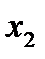
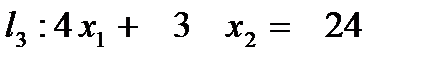
Дата добавления: 2017-02-01