Тема 10. Математическая модель межотраслевого баланса.

Модель межотраслевого баланса, разработанная профессором В. Леонтьевым (Гарвардский университет, США), имеет вид:

Если показатели представлены в некоторых фиксированных ценах, то есть, выражена стоимость продукции – то такой баланс называется стоимостным.

Общий вид межотраслевого баланса представлен в таблице.

Таблица Структура межотраслевого баланса.

Отрасли	P1	P2	…	Pn	Итого	Конечный продукт	Валовый продукт
P1	I	II
P2
…
Pn
Итого
Условно чистая продукция	III	IV
Валовый продукт

Каждая отрасль представлена в МОБ дважды: как производящая и как пот-ребляющая.

I квадрант – важнейшая часть межотраслевого баланса. В нем каждая отрасль представлена двояким образом, как элемент строки она выступает в роли поставщика производимой ее продукции. А как элемент столбца в роли потребителя продукции других отраслей экономической системы.

Отрасли как производителю соответствует строка таблицы, от-расли как потребителю соответствует столбец. На пересечении i-й строки и j-го столбца находится x_ij величинаi-й отрасли (в денежном выражении), израсходованной на производственные нужды j-й отрасли. Таким образом, первый раздел характеризует межотраслевые потоки сырья, материалов, энергии и т. д., обусловленные производственной деятельностью отраслей.

II квадрант МОБ состоит из двух столбцов. Столбец
Y - это конечная продукция отраслей. Конечная продукция включает в себя непроизводственное потребление (личное и общественное), возмещение выбытия основных фондов и накопление. Столбец Х содержит величины валового производства отраслей.

III квандрант представлен двумя нижними строками. Строка Х содер-жит те же самые величины, что и соответствующий столбец второго раздела. Строка V содержит величины условно-чистой продукции отраслей. Условно-чистая продукция включает в себя амортизационные отчисления и вновь созданную стоимость (заработную плату и прибыль).

IV квандрант МОБ не имеет непосредственного отношения к ана-лизу межотраслевых связей. Он характеризует перераспределительные отно-шения в народном хозяйстве и здесь рассматриваться не будет.

I и II квадрант отражают баланс между производством и потреблением.

I и III квадранты отражают стоимостную структуру продукции каждой отрасли.

Суммарный конечный продукт равен суммарной условной чистой продукции.

Вся производимая внутри экономической системы потребителя. Часть продукции потребляется в форме конечного продукта. Другая часть в форме суммарной потребления идет по производственные нужды отрасли входящей в экономическую систему.

Обозначения:

А = (a _{i j}) - матрица коэффициентов прямых затрат,

Х - вектор валовых выпусков,

Y - вектор конечного продукта.

E - единичная матрица n-го порядка,

x_ij - количество продукции

Строки показывают распределение продукции. Для любой i-й строки первого раздела справедливо соотношение:вся произведенная i-й отраслью продукция х_i (валовая продукция в денежном выражении) делится на промежуточную и конечную. Промежуточная продукция - это та часть валовой продукции i-й отрасли, которая расходуется другими отраслями в процессе осуществления ими собственных производственных функций.

Здесь (E - A) ^1 - матрица коэффициентов полных затрат.

Запись модели межотраслевого баланса в матричной форме:

AX + Y = X

Выразим

(E - A) X = Y

X = (E - A) ^1 Y

Элемент b _{i j} матрицы (E - A) ^1 характеризует потребность в валовом выпуске отрасли i, который необходим для получения в процессе материального производства единицы конечного продукта отрасли j. Благодаря этому имеется возможность рассматривать валовые выпуски x _i в виде функций планируемых значений y _j конечных продуктов отраслей:

.

Модель Леонтьева называется моделью «затраты-выпуск» потому, что отдельные отрасли рассматриваются в балансе двояко:

1. как выразители совокупного спроса и покупатели материальных благ и услуг, предложенных другими отраслями (затраты) - это столбцы баланса;

2.как выразители совокупного предложения и продавцы материальных благ и услуг, которые они предоставляют сами другим отраслям (выпуск) - это строки баланса.

Модель затраты - выпуск связана с системой национальных счетов (СНС), принятой в странах с рыночной экономикой.

Построение балансовой таблицы – это I этап решения задачи методом математического моделирования.

Построения таблицы:

А) Вписаны объекты изучения

Б) Установлены существенные связи между ними

В) Собрана статистическая информация.

Г)

Д) Баланс между производством и потреблением

E) Стоимостная структура i отрасли

Ж) Промежуточный продукт экономической системы

	P1	P2	P3	∑	y	x
P1
P2
P0
∑
V
X

Стоимость всей произведенной j-й отраслью продукции х_j состоит из текущих производственных затрат и условно-чистой продукции v_j.

Суммарный конечный продукт равен суммарной условно-чистой продукции.

Зная суммарный конечный продукт или, что то же, суммарную условно-чистую продукцию, можно определить национальный доход. Он равен разности суммарного конечного продукта и амортизационных отчислений, направляемых на возмещение выбытия основных фондов.

р1
р2

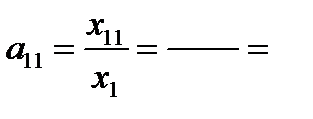
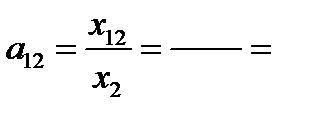
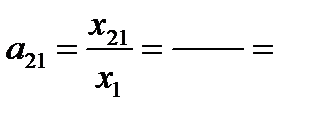
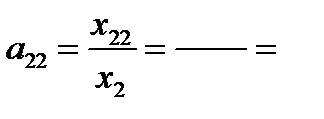
Матрица коэффициентов прямых затрат

сумма коэффициентов по столбцам

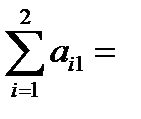
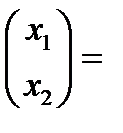
Решение:

Матрица прямых затрат

вектор-столбец готовой продукции

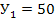
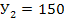
Пункт 1

Система линейных уравнений межотраслевого баланса

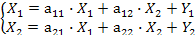
Экономическое истолкование: Выпускаемая каждым экономическим объектом продукция частично потребляется другими объектами системы в качестве сырья, полуфабрикатов и т.п. (внутрипроизводственное потребление), а часть идет на личное и производственное потребление вне данной экономической системы (внепроизводственное потребление в виде конечного продукта)

Пункт 2

Найдем валовые выпуски отраслей х1 и х2

Для этого найдем разность единичной матрицы 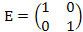и матрицы А

Найдем определитель этой матрицы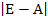

Найдем обратную матрицу по формуле

= =

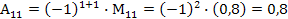
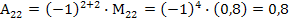
=204,92

Таким образом, чтобы удовлетворить конечный спрос, валовой выпуск первой отрасли должен составить , второй отрасли 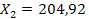единиц

Пункт 3

Найдем коэффициенты полных затрат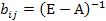

стоимость части валового продукта , которая необходима ,для выпуска ею единицы конечного продукта

Пункт 4

Изменение валовых выпусков всех отраслей при увеличении конечного продукта первой отрасли на

Матрица прямых затрат

вектор-столбец готовой продукции

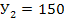
Найдем разность единичной матрицы 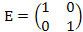и матрицы А

Найдем определитель этой матрицы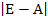

Найдем обратную матрицу по формуле

= =

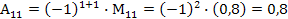
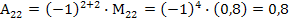
=205,08

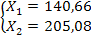
Таким образом, чтобы удовлетворить конечный спрос, валовой выпуск первой отрасли должен составить , второй отрасли единиц

Задание

Дана матрица коэффициентов прямых затрат

Определить матрицу коэффициентов и определить, будет ли матрица продуктивной.

Решение:

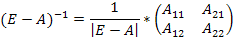
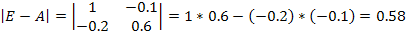
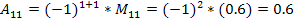
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:lang w:val="EN-US"/></w:rPr><m:t>*(-0.1)=0.1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00DE5BAB"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:lang w:val="EN-US"/></w:rPr><m:t>*(1)=1</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00CA685D"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">

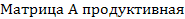
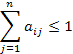
0.4+0.2<1 0.1+0.8<1 0.4+0.1≤1 0.2+0.8≤1 Продуктивная

0.3+0.8>1 0.7+0.1<1 0.3+0.7≤1 0.8+0.1≤1 Непродуктивная

Задание

Три судна доставили в порт 6000 т чугуна, 4000 т железной руды и 3000 т апатитов. Разгрузку можно производить как непосредственно в железнодорожные вагоны для последующей доставки потребителям, так и на портовые склады. В вагоны можно разгрузить 8000 т, а остаток груза придется направить на склады. Необходимо учесть, что поданные в порт вагоны не приспособлены для перевозки апатитов. Стоимость выгрузки 1 т в вагоны составляет соответственно 4,30, 5,25 и 2,20 ден. ед.

Задание

Пусть дана модель МОБ Леонтьева “затраты - выпуск” X = AX +Y.

Найти вектор конечной продукции Y при заданном X, где

;

Решение.

Y = (E - A) X,

где E - единичная матрица третьего порядка.

,

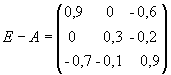значит,

.

Задание

Пусть дана модель МОБ “затраты-выпуск”. Определить, будет ли продуктивной матрица технологических коэффициентов A. Найти вектор валовой продукции X при заданном Y, где

.

Решение.

Для решения вопроса о продуктивности матрицы A следует найти собственные значения этой матрицы. Составим характеристическое уравнение:

,

или

(0,125 - )² - 0,140625 = 0

Следовательно, ₁ = 0,5; ₂ = - 0,25. Оба корня по модулю меньше единицы, значит, матрица технологических коэффициентов A продуктивная. Для определения вектора валовой продукции X имеем формулу
X = (E - A) ^1 Y. Найдем обратную матрицу для матрицы

.

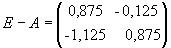Обозначим B = E-A, тогда

.

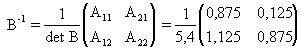Следовательно,

.

Из этой модели получают следующие виды равновесия:

отраслевое равновесие Сумма счетов затрат отрасли равна сумме счетов выпуска ее продукции.

межотраслевое равновесие, например для обрабатывающей и добывающей промышленности.

Общее равновесие Совокупное предложение и совокупный спрос на товары равны.

Задача

В модели Леонтьева дана матрица прямых затрат А и вектор конечного спроса у.

Требуется найти вектор х валового выпуска, обеспечивающий данный спрос.

Данные к выполнению задания: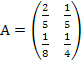

Решение:

Матрица прямых затрат

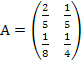
вектор-столбец готовой продукции

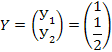
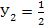
Найдем разность единичной матрицы 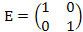и матрицы А

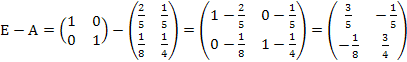
Найдем определитель этой матрицы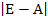

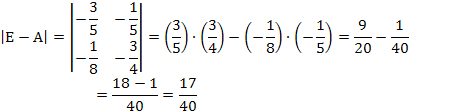
Найдем обратную матрицу по формуле

=

=

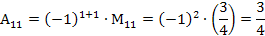
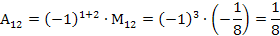
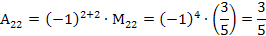
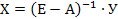
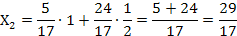
Таким образом, чтобы удовлетворить конечный спрос, валовой выпуск первой отрасли должен составить 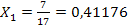, второй отрасли единиц

Задача

Требуется определить конечный продукт фирмы 1 и фирмы 2, если известны объемы совокупных продуктов С1 и С2 и матрица коэффициентов прямых затрат А

Данные к выполнению задания:

С1=200 С2=400 а11=10 а22=30 а12=50 а21=72

Решение:

Определим суммарные затраты на производство продукции первой и второй фирмы

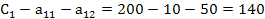
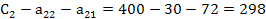
Найдем отношения и матрицу коэффициентов прямых затрат

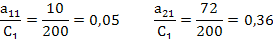
Матрица коэффициентов прямых затрат имеет вид

Запишем соответствующие уравнения:

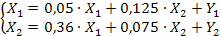
Запишем вектор-столбец объемов производства

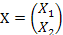
Запишем вектор-столбец готовой продукции

=

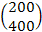
Модель Леонтьева в матричной форме Х=АХ+У

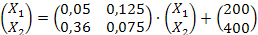
X-AX=Y

(E-A)X=Y

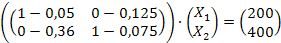
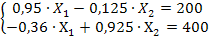
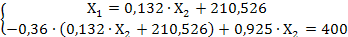
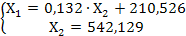
Таким образом, чтобы удовлетворить конечный спрос, совокупный продукт 1 фирмы должен составить 281, 859 единиц, 2 фирмы 542, 129 единиц

Задания для самостоятельного решения по теме №10

Таблица

Восстановить пропущенные значения в таблице межотраслевого баланса.

	P1	P2	∑	y	x
P1
P2
∑
V
X

Таблица

	P1	P2	∑	y	x
P1
P2
∑
V
X

Таблица

	P1	P2	P3	∑	y	x
P1
P2
P3
∑
V
X

Таблица

	P1	P2	P3	∑	y	x
P1
P2
P3
∑
V
X

Итоговая контрольная работа по курсу ЭММ

Задание 1 Составить математическую модель и решить задачу линейного программирования.

a) Графическим методом

b) Симплекс-методом,

c) Определить количество дефицитных ресурсов и изменение ресурса

d) Составить двойственную задачу и записать ее решение

Вариант 1

Cырье	А	Б	Запас
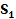
Прибыль			max

Вариант 2

Cырье	А	Б	Запас
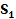
Прибыль			max

Задание 2. На трех базах А₁, А₂, А₃ имеется однородный груз в количестве а₁, а₂, а₃ единиц. Этот груз нужно перевезти в пять пунктов В₁, В₂, В₃, В₄, В₅ в количестве b₁, b₂, b₃, b₄, b₅ единиц соответственно. Затраты на перевозку груза между пунктами поставок и потребления заданы матрицей тарифов С:

.

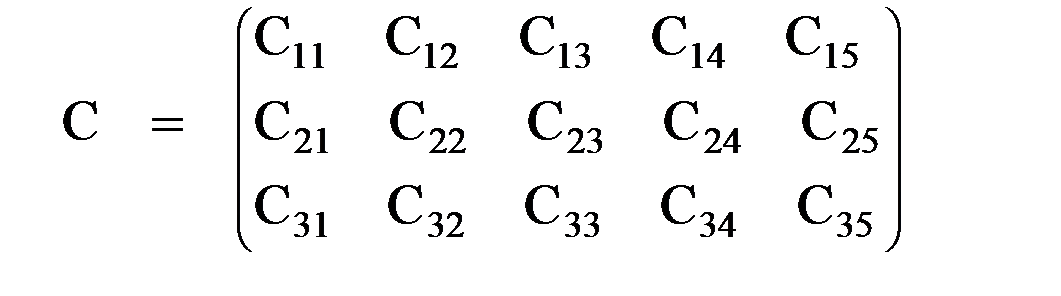Спланировать перевозки так, чтобы их общая стоимость была минимальной.

Вариант1

Вариант2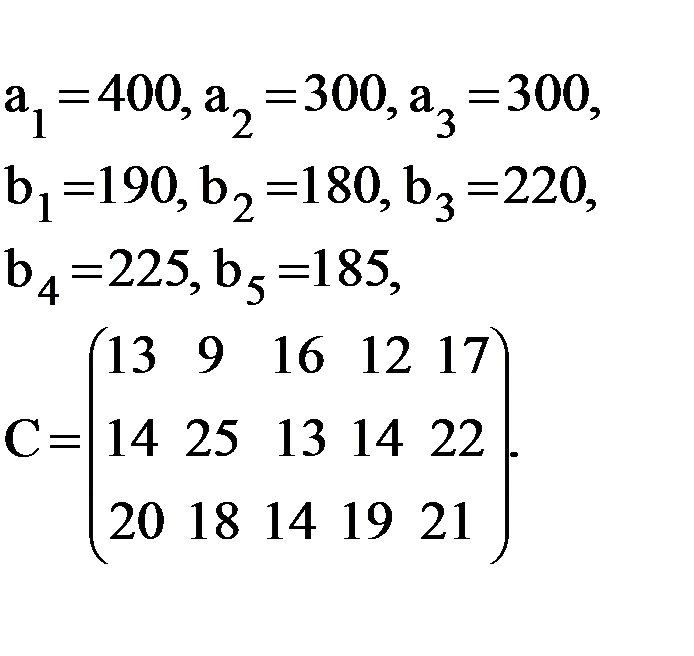

Задание 3. Составить экономико-математическую модель. Вариант 1. Торговое предприятие реализует товары Т₁, Т₂, Т₃, Т₄, используя при этом площади торговых залов, оборудование и время обсуживающего персонала. Затраты на продажу одной партии товара каждого вида, их объемы и прибыль, получаемая от реализации каждой партии товара, приведены в таблице. Найти оптимальную структуру товарооборота, обеспечивающую предприятию максимальную прибыль.

Ресурсы	Запас ресурса	Затраты ресурсов на товары
Т1	Т2	Т3	Т4
Время, чел.-ч		0,5	0,7	0,6	0,5
Оборудование, маш.-ч		0,3	0,4	0,2	0,3
Площадь, м^2		0,1	0,3	0,2	0,2
Прибыль, ден. ед.

Вариант 2 На предприятии освоены четыре технологии производства основной продукции. В таблице указаны запасы потребляемых ресурсов, затраты их в течение месяца и объемы выпуска готовой продукции. Установить такое время работы предприятия по каждой технологии, при котором выпуск продукции будет максимальным, а расход ресурсов не превысит их наличия.

Ресурсы	Запасы ресурсов	Расход ресурса при технологии
I	II	III	IV
Р1
Р2
Р3

Литература:

Основная:

1) Бережная, В.Б. Математические методы моделирования экономических систем [текст]: Учебное пособие/В.Б. Бережная, В.И. Бережной. – М.: Финансы и статистика, 2001. – 368 с.

2) Исследование операций [текст]/Под ред. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 388 с.

3) Калихман, И.Л. Динамическое программирование в примерах и задачах [текст]: Учебник/ И.Л. Калихман, М.А. Войтенко. – М.: Высшая школа, 1979.. – 296 с.

4) Конюховский, П.В. Математические методы исследования операций в экономике [текст]/ П.В. Конюховский. – СПб: Питер, 2000. – 208 c.

5) Сборник задач по высшей математике для экономистов [текст]: Учебное пособие/ Под ред. В. И. Ермакова. – М.: ИНФРА-М, 2001. – 575 с.

6) Общий курс математики для экономистов [текст]: Учебник/ Под ред. В. И. Ермакова. – М.: ИНФРА-М, 2002. – 656 с.

7) Шапкин, А.С. Математические методы и модели исследования операций [текст]: Учебник/А.С. Шапкин, Н.П. Мазаев. – М.: Издательско-торговая корпорация «Дашков и К», 2004. – 400 с.

8) Экономико-математические методы и прикладные модели [текст]: Учебное пособие /Под ред. В.В. Федосеева. – М.: ЮНИТИ, 2002. – 391 с.

Дополнительная:

1) Ашманов, С.А. Математические модели и методы в экономике [текст]: Учебник / С.А. Ашманов. – М.: Высшая школа, 1980. – 354 c.

2) Бусленко Н. П. Моделирование сложных систем. М. Наука 1978г.

3) Вентцель, Е. С. Исследование операций [текст]/ Е. С. Вентцель. – М.: Советское радио, 1972. – 552 c.

4) Дубров А.М., Лагоша Б.А., Хрусталев Е. Ю. Моделирование рисковых ситуаций в экономике и бизнесе. М. Финансы и статистика 1999г.

5) Жданов С. Экономические модели и методы управления. М.Эльта 1998г.

6) Карасев А.И., Кремер Н.Ш., Савельева Т.Н. Математические методы и модели в планировании. М. Экономика. 1987г

7) Малыхин В.И. Математическое моделирование экономики. М. Из-во УРАО 1998г.

8) Справочник по математике для экономистов [текст]/Под ред. В.И. Ермакова. – М.: Высшая школа, 1987. – 336.

9) Петросян Л. А., Зенкевич Н. А., Семина Е. А. Теория игр. М.,1998.

10) Терехов Л.Л. Экономико- математические методы. М. Статистика 1988г.

11) Шелобаев, С.И. Математические методы и модели в экономике [текст]: Учебное пособие/ С.И. Шелобаев. – М.: ЮНИТИ, 2001. – 367 с.

12) Шикин, Е. В. Математические методы и модели в управлении [текст]: Учебное пособие/Е.В. Шикин, А.Г. Чхартишвили. - М.: Дело, 2000. – 440 с.

Интернет-ресурсы

1) rmat-english.narod.ru/rmat/kafedry/strategia/kluchnikov_14.doc

Дата добавления: 2017-02-01