Контрольні запитання

1. Що називається похідною другого, третього,n-го порядку?

2. Що називається диференціалом другого, третього,n-го порядку?

3. Як шукають похідну та диференціал вищих порядків?

4. Сформулюйте правила відшукання похідних вищих порядків суми, різниці, добутку функцій.

5. Сформулюйте і доведіть теорему Ролля, який її геометричний зміст?

6. Сформулюйте і доведіть теорему Лагранжа, який її геометричний зміст?

7. Сформулюйте і доведіть теорему Коші.

8. Сформулюйте перше правило Лопіталя. Коли його зручно застосовувати?

9. Сформулюйте друге правило Лопіталя. Коли його зручно застосовувати?

10. Як розкрити невизначеності типу , , ; .

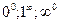Тема 2.3. Застосування похідної до дослідження функції

Мета: вивчити основні застосування похідної функції для її дослідження.

План.

1. Умови монотонності функції.

2. Найбільше та найменше значення функції. Застосування естремумів функції в задачах.

3. Проміжки опуклості та вгнутості.

4. Асимптоти графіка функції.

5. Загальна схема побудови графіка.

1. Теорема 1. Нехай функція f(x) неперервна на проміжку <a;b> і диференційовна на інтервалі (a;b). Для того, щоб функція була сталою необхідно і досить, щоб для всіх xÎ(a;b).

Доведення.

Якщо функція f(x) стала на проміжку, то для всіх xÎ(a;b). Цим доведено необхідність.

Доведемо достатність. Нехай для всіх xÎ(a;b). Візьмемо будь- яку фіксовану точку x₀Î(a;b). Тоді за теоермою Лагранжа в довільній точці xÎ(a;b) маємо

.

Отже, функція стала на проміжку. Теорему доведено.

Теорема 2. Нехай функція f(x) неперервна на проміжку <a;b> і диференційовна в інтервалі (a;b). Для того, щоб функція f(x) не спадала (не зростала) на проміжку <a;b> необхідно і досить, щоб () для всіх xÎ(a;b).

Доведення. Нехай функція f(x) не спадає не проміжку <a;b> і нехай xÎ(a;b). Тоді при Dx>0 маємо

,

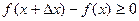звідси і

Необхідність доведено.

Припустимо тепер, що для всіх xÎ(a;b). Нехай x₁ і x₂- довільні точки проміжку <a;b>, x₁ < x₂. За теоермою Лагранжа, умови якої на відрізку виконуються, дістанемо

, де x₁<c< x₂.

тобто f (x₂)³f(x₁). Функція на проміжку <a;b> не спадає. Аналогічно доводиться теорема для випадку, коли f(x) не зростає на проміжку.

Теорема 3. Нехай функція f(x) неперервна на проміжку <a;b> і диференційовна в інтервалі (a;b). Для того, щоб функція f(x) була зростаючою (спадною) на проміжку <a;b> необхідно і досить, щоб () для всіх xÎ(a;b), причому ті точки, де не складали ніякого відрізка.

Доведення проводимо на основі припущення від супротивного і використання теоерми 2.

2. Вважають, що функція f(x) має максимум (мінімум) в точці x₀, якщо існує окіл цієї точки (x₀-d; x₀+d), такий, що для всіх xÎ(x₀-d; x₀+d) правильна нерівність f(x)<f(x₀) (f(x)>f(x₀)).

Максимуми та мінімуми функції називаються її екстремумами. Екстремум деколи називають локальним, щоб підкреслити, що це максимум чи мінімум на якомусь невеликому проміжку, а не для всієї області визначення функції.

Теорема (необхідна ознака екстремуму функції). Якщо функція має в точці екстремум і якщо в цій точці існує похідна, то ця похідна рівна нулю.

Доведення. Нехай для означеності функція f(x) має в цій точц імаксимум. Тоді існує окіл (x₀-d; x₀+d) цієї точки такий, що f(x)<f(x₀) для всіх xÎ(x₀-d; x₀+d). Тоді f(x₀+Dx)<f(x₀) для всіх x₀+Dx Î(x₀-d; x₀+d), Dx¹0.

Якщо Dx>0, то <0,

отже,

.

Якщо ж Dx<0, то >0,

і, отже,

.

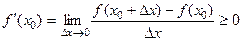Звідси робимо висновок що .

Точки, в яких похідна рівна нулю, називаються стаціонарними. Остання теорема дає можливість шукати точки екстремуму серед стаціонарних точок. Тобто, спочатку знайдемо похідну функції, прирівняємо її до нуля і перевіримо на максимум чи мінімум, розглянувши поведінку функції в околі точки.

Теорема 2. Нехай функція f(x) диференційовна в околі точки x₀, можливо за винятком самої точки, в якій функція неперервна. Якщо при переході через точку x₀ похідна функції міняє знак з плюса на мінус, то функція має в цій точці максимум, а якщо з мінуса на плюс, то – мінімум.

Доведення.

Нехай для означеності похідна змінює знак з плюса на мінус. Тоді

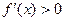для всіх xÎ(x₀-d; x₀) і 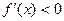для всіх xÎ(x₀; x₀+d).

Тоді на проміжку (x₀-d; x₀) функція зростає, а на проміжку (x₀; x₀+d)- спадає. Отже, для всіх

xÎ(x₀-d; x₀+d) правильна нерівність f(x)<f(x₀), а це означає, що функція має в точці х₀ максимум.

Аналогічно доводимо і для випадку, коли функція міняє знак з мінуса на плюс.

Про наявність екстремуму функції можна судити і по другій похідній в стаціонарній точці.

Теорема 3. Нехай функція f(x) диференційовна в околі своєї стаціонарної точки x₀, а в самій стаціонарній точці має другу похідну. Тоді, якщо то функція має в цій точці макасимум, а якщо , то – мінімум.

В багатьох задач вимагають знайти максимум чи мінімум функції на відрізку. В таких випадках користуємось наступним правилом:

1) шукаємо стаціонарні точки на інтервалі, що відповідає заданому відрізкові;

2) досліджуємо їх на екстремуми;

3) шукаємо значення функції в крайніх точках відрізка;

4) порівнюємо значення функції в крайніх точках та екстремуми і визначаємо з них найменше- це буде мінімум, та найбільше- це буде максимум.

3. Нехай функція f(x) диференційовна в інтервалі (a;b). Тоді в кожній точці цього інтервалу існує дотична до кривої і ця дотична не паралельна осі Oy.

Вважають, що крива y=f(x) обернена опуклістю вгору (вниз) в інтервалі (a;b), якщо вона лежить нижче (вище), ніж будь- яка дотична, проведена в довільній точці цієї кривої (зрозуміло, виключаючи саму точку дотику, яка лежить на кривій). Часто кажуть, що крива, обернена опуклістю вгору називається опуклою, крива, обернена опуклістю вниз- вгнутою.

Теорема 1. Нехай функція f(x) в інтервалі (a;b) має похідну другого порядку. Якщо для всіх xÎ(a;b), то крива y=f(x) в інтервалі (a;b) обернена опуклістю вниз (вгору).

Доведення.

Нехай для всіх xÎ(a;b). Проведемо дотичну до кривої y=f(x) в довільній точці x₀Î(a;b). Її рівняння має вигляд

. (1)

Якщо a<x<x₀, то, знайшовши з рівняння (1) і двічі застосувавши теорему Лагранжа, дістанемо

=

,

де x<c₁<c₂<x₀.

Оскільки x-x₀<0, c₁-x₀<0 і, внаслідок умови теореми, , то

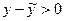або ,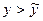

Тобто крива y=f(x) лежить вище, ніж дотична в інтервалі (a;x₀,)..

Якщо ж x₀<x<b, то

=

,

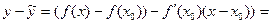де x₀<c₃<c₄<x.

Оскільки x-x₀>0, c₃-x₀>0 і внаслідок умови теореми, то,

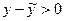або .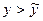

Тобто крива лежить вище, ніж дотична і в інтервалі (x₀;b).

А це означає, що в інтервалі (a;b) крива обернена опуклістю вниз.

Аналогічно доводимо, що коли для всіх xÎ(a;b), то крива обернена опуклістю вгору.

Ця теорема дає достатню умову для того, щоб крива була обернена опуклістю вгору (вниз) в інтервалі (a;b).

Наслідок 1. Нехай в окoлі точки c функція f(x) має другу похідну, неперервну в точці c. Якщо (), то в досить малому околі точки c крива обернена опуклістю вниз (вгору).

Доведення.

Дійсно, якщо функція 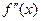неперервна в точці c, то вона зберігатиме знак в досить малому околі цієї точки, буде додатньою, якщо і від’ємною, якщо . За теоремою 1, крива буде обернена опуклістю вниз, якщо і опуклістю вгору, якщо .

Інтервал, в якому крива обернена опуклістю вниз (вгору) називається інтервалом опуклості вниз (вгору) цієї кривої.

Нехай функція f(x) диференційована в інтервалі (a;b), за винятком можливо точки c Î(a;b), в якій неперервна, і нехай у точці c існує дотична. Точка c називається точкою перегину кривої, якщо існує такий окіл точки c, що в лівій половині цього околу крива обернена опуклістю вниз (вгору), а в правій вгору (вниз).

Дамо необхідну умову для точки перегину.

Теорема 2. Нехай функція f(x) в околі точки c має похідну другого порядку, неперервну в точці c. Якщо точка c є точкою перегину кривої y=f(x), то .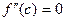

Доведення.

Доведемо методом від супротивного. Припустимо, що . Тоді в результаті наслідку з теореми 1, знайдеться окіл точки c, в якому крива буде опуклою, якщо або вгнутою, якщо . А це суперечить умові теореми, за якою точка c є точкою перегину.

Отже, 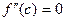і теорему доведено.

Теорема 3. Нехай функція f(x) має похідну другого порядку , причому 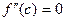. Якщо при переході точки x через точку c змінює знак, то точка (c; f(c)) є точкою перегину.

Доведення.

Нехай, наприклад, для xÎ(c-d; c) і для xÎ(c; c+d), де d>0, тобто нехай при перході x через точку c, 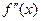змінює свій знак з мінуса на плюс. Тоді за теоремою 1 в інтервалі (c-d; c) крива опукла, а в інтервалі (c; c+d)– вгнута. Оскільки 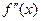існує в околі точки c, то в цьому околі існує і , зокрема існує , тобто в точці c існує дотична до кривої (причому вона не паралельна до осі). Тому точка c є точкою перегину кривої.

З вищедоведених теорем маємо правило знаходження інтервалів опуклості та вгнутості:

Щоб знайти інтервали опуклості (вгнутості) і точки перегину кривої, треба знайти похідну другого порядку від функції f(x). Після цього розв’язати рівняння 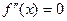. Корені цього рівняння, а також точки в яких друга похідна не існує є точками, що можуть бути точками перегину. Після цього, користуючись теоремою перевіряємо поведінку 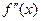при проходженні через ці точки. Якщо 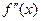змінює знак, то ця точка буде точкою перегину, а інтервали, що лежать між точками перегину будуть інтервалами опуклості чи вгнутості.

4. Нехай функція f(x) визначена в інтервалі (a; +¥) (в інтервалі (-¥; а)). Пряма

y=kx+b (1)

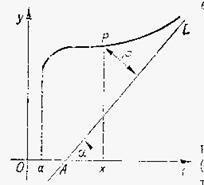називається асимптотою кривої y=f(x), якщо відстань точки P(x; f(x)), яка лежить на кривій, до цієї прямої прямує до нуля при (при ).

Теорема. Нехай функція f(x) визначена в інтервалі (a; +¥) (в інтервалі (-¥;а)). Для того, щоб пряма (1) була асимптотою кривої y=f(x), необхідно і досить, щоб

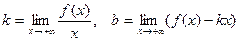, (2)

().

Доведення.

Розглянемо випадок, коли функція f(x) визначена в інтервалі(a; +¥). (Коли функція визначена в інтервалі (-¥;b) – міркування аналогічні).

Доведемо необхідність умов (2). Нехай пряма (1) є асимптотою кривої y=f(x). Відстань від точки P(x; f(x)), що лежить на цій кривій, до прямої (1) дорівнює добутку абсолютної величини різниці ординат у точці x кривої і прямої на косинус a, де a – кут нахилу прямої (1) з додатним напрямом осі Ox, , тобто

.

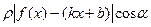Оскільки 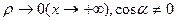і a не залежить від x, то

.

Звідси

І

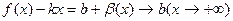
Тобто правильні рівності (2).

Доведемо достатність умов (2). Нехай мають місце рівності (2), де k і b- скінченні числа. Покажемо, що пряма (1), де k і b визначаються з рівностей (2), є асимптотою кривої y=f(x). З (2) маємо

Тобто абсолютна величина різниці ординат у точці x кривої y=f(x) і прямої (1) прямує до нуля при x®+¥. Проте тоді при x®+¥ прямує до нуля і відстань точки P(x,f(x)), що належить кривій до прямої (1). Отже, пряма (1) є асимптотою кривої.

Теорему доведено.

Асимптоти кривої, які записані у вигляді (1) називають похилими асимптотами.

Нехай функція f(x) визначена в околі точки x₀ і нехай

або ,

або і те, і друге. Тоді пряма x=x₀ називається вертикальною асимптотою.

5. Повне дослідження функції рекомендується проводити за такою схемою:

1. Визначити область існування функції. Встановити точки розриву і інтервали неперервності функції. Дослідити функцію на парність, непарність, періодичність.

2. Знайти точки максимуму та мінімуму функції, обчислити значення функції в цих точках. Встановити інтервали монотонності функції.

3. Знайти точки перегину графіка функції, обчислити значення функції в цих точках.

4. Встановити інтервали опуклості графіка функції.

5. Знайти асимптоти графіка функції. Обчислити граничні значення функції в точках, межових для області його існування.

6. Побудувати графік функції.

Зауважимо, що зручно після кожного пункту схеми наносити точки та їх значення на координатній площині, для того, щоб накреслення графіка функції йшло паралельно до дослідження.

Дата добавления: 2017-02-01