Тема 3.2. Частинні похідні. Диференнційовність та диференціал

Контрольні запитання

1. Що називається функцією з кількома змінними?

2. Що називається областю визначення, областю значень, аргументами?

3. Що таке лінія, поверхня рівня?

4. Що називається границею функції кількох змінних?

5. Яка функція називається неперервною в точці, на області?

Мета. Дати поняття диференційовності функції кількох змінних та її повного диференціала. Означити частинні похідні,їх геометричний та механічний зміст. Дати поняття похідної складеної функції від декількох змінних.

План.

1. Частинні похідні та їх геометрична і механічна інтерпритація.

2. Диференнційовність. Повний диференціал.

3. Диференціювання складних функцій.

4. Диференціювання функцій, заданих неявно.

1. Нехай задано функцію z=f(x,y) і деяка точка (x,y) ÎD. Якщо змінна функції z проходить тільки по одній змінній, наприклад x, при фіксованому значенні другого аргумента y, то функція отримає приріст

Цей приріст називають частинним приростом функції f(x,y) по аргументу x.

Розглядаючи зміну функції z за одним аргументом при фіксованому іншому ми фактично переходимо до функції однієї змінної.

Якщо існує скінченна границя

,

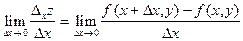то вона називається частинною похідною функції f(x,y) по аргументові x і позначається одним із символів і т.д.

Аналогічно визначаємо частковий приріст z по y:

і частина похідна має вигляд:

.

За означенням кожна частина похідна є фактично похідною функції від одної змінної, тому при їх обрахування можна користуватися правилами, знайомими нам з теорії диференціювання функції однієї змінної, вважаючи при цьому другу змінну постійною.

Приклад.

Знайти частинні похідні функції .

Розв’язання.

Маємо (y - фіксоване), (x - фіксоване).

Аналогічно вводимо поняття частинних похідних для функції трьох і більшої кількості змінних.

Частинні похідні функції декількох змінних обраховуються за припущенням, що змінюється лише одна змінна, а всі інші залишаються фіксованими.

Приклад. Знайдемо частинні похідні функції .

Розв’язання.

Маємо (y, z -фіксовані), (х, z -фіксовані), (х, y -фіксовані).

Геометричним змістом частинної похідної функції кількох змінних є наступне твердження:

Частинна похідна по x в точці М₀ дорівнює кутовому коефіцієнтові дотичної, проведеної до лінії перетину поверхні площиною в точці Р₀ (x₀, y₀, f(x₀,y₀)).

Для функцій більшої кількості змінних геометричної інтерпритації похідної не існує.

Частна похідна функції кількох змінних має той самий механічний зміст, що й похідна функції однієї змінної. Це - швидкість зміни функції відносно зміни одного з аргументів.

2. Добуток частинної похідної на приріст відповідної незалежної змінної називається частинним диференціалом. Частинні диференціали позначаються так:

, .

Сума частинних диференціалів по всіх незалежних змінних називається повним диференціалом. Для функції двох незалежних змінних повний диференціал має вигляд

.

Приклад. Знайти повний диференціал функції .

Розв’язок. Знайшовши частинні похідні і застосувавши вищевказану формулу, маємо

(1)

Функція, яка має повний диференціал в заданій точці називається диференційовною в цій точці. Функція, яка має повний диференціал в кожній точці області називається диференційовною в цій області.

Так як і у випадку функції однієї змінної, з диференційовнності функції слідує її неперервність, але не навпаки.

Сформулюємо достатню умову диференційовності функції.

Теорема. Якщо функція z=f(x,y) має неперервні частинні похідні по незалежних змінних в данній області, то вона диференційована в цій області і її диференціал виражається формулою (1).

Аналогічно до функції однієї змінної можна показати, що повний диференціал представимий у виді двох доданків: перший з яких лінійний відносно Dх, Dy, а другий є нескінченно малою функцією вищого порядку відносно Dx, Dy.

Для функції більшої кількості змінних поняття диференціалу вводиться аналогічно.

Покажемо, як застосувати повний диференціал до наближених обчислень.

,

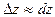Наприклад, обчислимо .

, , .

, ,

, .

= + .

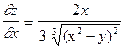3. Нехай маємо функцію z=f(u,v), де u=j(x,y), v=y(x,y). Тоді функція z є складеною функцією від двох незалежних змінних x,y. Нехай функції f, j, y мають неперервні частинні похідні при всіх аргументах, тоді справедливі рівності.

; .

Приклад.

Продиференціювати функцію , якщо , .

Розв’язування.

.

.

Отже, ;

.

Нехай маємо функцію z=f (x,u,v), де u=j(x), v=y(x). Тобто фактично маємо функцію z=f(x, j(x), y(x)). Формула повної похідної має вигляд:

.

4. Нехай функція однієї змінної задана неявно, тобто записана у виді

F(x,y)=0, (1)

де y=f(x). Перепишемо у вигляді

F(x,f(x))=0. (2)

Теорема 1. Нехай функція F(x,y) визначена, неперервна і має неперервні частинні похідні в деякому околі точки P₀(x₀,y₀). Крім того, в цій точці , , тоді в деякому околі т. P₀(x₀,y₀) рівняння (1) визначає однозначну функцію, яка є неперервна і диференційована в деякому околі т. х₀.

Знайдемо повну похідну від функції, яка міститься в лівій частині тотожності (2).

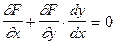Þ .

Розглянемо функцію від двох змінних: z=f(x;y). Її можна переписати у вигляді

F(x,y,z)=0 (3)

або

F(x,y,f(x,y))=0 (4)

Теорема 2. Нехай функція F(x,y,z) визначена, неперервна і має неперервні частині похідні в деякому околі точки М₀(x₀, y₀, z₀). При цьому ця точка задовільняє умови: , . Тоді рівність (3) визначає в деякому околі точки М однозначну функцію z=f(x,y), z₀ =f(x₀,y₀), ця функція неперервна, має неперервні частинні похідні і можна довести, що справедливі наступні формули:

Дата добавления: 2017-02-01