Тема 3.3. Частинні похідні та диференціали вищих порядків. Застосуваня частинних похідних

Контрольні запитання

1. Що називається частинною похідною?

2. Як обрахувати частину похідну?

3. Що є геометричним, механічним змістом похідної функції від кількох змінних?

4. Що називається частинним диференціалом функції кількох змінних?

5. Що називається повним диференціалом функції кількох змінних?

6. Яка достатня умова неперервності функції?

7. Наведіть приклад застосування повного диференціала до наближених обчислень.

8. Як продиференціювати складену функцію від кількох змінних?

9. Як продиференціювати неявно задану функцію від кількох змінних?

Мета: Оволодіти апаратом частинних похідних для розв’язування деяких прикладних задач.

План.

1. Частинні похідні та диференціали вищих порядків.

2. Поняття похідної за напрямком. Градієнт.

3. Дотична площини і нормаль до поверхні.

4. Поняття про екстремум функції 2-ох незалежних змінних.

5. Умовний екстремум. Найбільше і найменше значення функції.

1. Частинні похідні функції від кількох змінних є в свою чергу функціями від тих самих змінних, тому від них також можна визначити частинні похідні. Таким чином ми отримуємо частинні похідні 2-го порядку. Диференціювання таких частинних похідних 2-го порядку приведе в свою чергу до частинних похідних 3-го порядку і т.д.

У випадку функції змінних z=f(x;y) отримаємо:

- частинні похідні 1-го порядку:

(1)

- частинні похідні 2-го порядку:

(2)

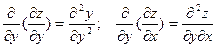
Для таких похідних використовуються також позначення:

(3)

Друга і четверта похідні в (2) і (3) називаються мішаними.

Без доведння приймемо теорему 1:

Якщо частинні похідні вищого порядку неперервні, то мішані похідні одного і того ж порядку, що відрізняються тільки порядком диференціювання, рівні між собою.

Приклад: Обчислити часинні похідні до 3-го порядку включно для функції U=x⁴+x²y²+y⁵+1.

Розв’язування.

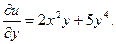
(Порівняйте 2-гу і 3-тю формули).

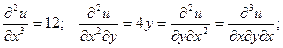
Диференціалом другого порядку від функції z=f(x;y) називають диференціал від її повного диференціалу

d²z-d(dz). (4)

Аналогічно:

d³z=d(d²z);

dⁿz=d(d^n-1z).

Якщо x,y-незалежні змінні і функція має неперервні частинні похідні, то справедливі формули:

і взагалі, має місце символічна формула:

(5)

яка розкривається по біномінальному закону.

Якщо ж x i y - функції від однієї чи декількох незалежних змінних, то повний диференціал другого порядку шукається з застосуванням (4) і . (6)

Приклад: Знайти повні диференціали 1-го і 2-го порядків для

z=4^x2-6xy+5^y2.

Розв’язування.

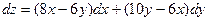
Далі

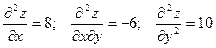
2. Означення. Похідною функцією z=f(x;y) в даному напрямі називають границею

де: - значення функції в точках Р₁ і Р відповідно,

Якщо функція z-диференційовна, то

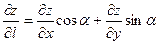(7)

де: a-кут між вектором l і віссю Ox.

У випадку функції трьох змінних u=f(x;y;z) похідна по заданому напрямку обраховується як

,

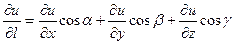де: a,b,g-кути між напрямним вектором і Ox, Oy, Oz.

Похідна по напрямку характеризує швидкість зміни функції в даному напрямі.

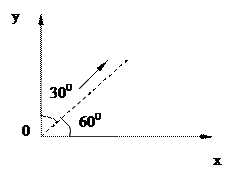Приклад. Знайти похідну функцій z=x²-xy-2y² в точці Р(1;2) в напрямі, що утворює з віссю Ох кут 60⁰.

Розв’язування.

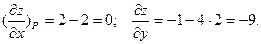
Тоді:

Мінус вказує, що функція в даній точці і в даному напрямі зменшується.

Означення. Градієнтом функції z=f(x;y) називається вектор, проекціями якого на відповідні координатні осі є частинні похідні даної функції:

(8)

Градієнт функції в кожній точці напрямлений по нормалі до відповідної лінії рівня функції. Він виражає напрям найбільшого росту функції в даній точці. Тобто при l=grad z похідна 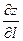має найбільше значення

Для функції 3^х змінних u=f(x;y;z)

Градієнт функції 3-х змінних в кожній точці напрямлений по нормалі до поверхні рівня, що проходить через цю точку.

3. Означення 1: Дотичною площиною до заданої поверхні в точці М називається площина, що містить всі дотичні до кривих, проведених на поверхні через точку М.

Означення 2: Нормаллю до поверхні називається пряма, що проходить через точку дотику М і перепендикулярна до дотичної площини.

Якщо поверхня задана рівнянням F(x;y;z)=0, то рівняння дотичної площини в точці М(x₀;y₀;z₀) має вигляд

(9)

де: 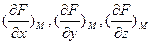-значення частинних похідних в точці М; x; y; z -поточні координати дотичної площини.

Рівняння нормалі:

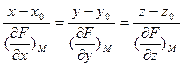, (10)

де x, y, z – поточні координати нормалі.

Якщо рівняння поверхні задане в явному вигляді z=f(x;y), то рівняння дотичної площини в т. М(x₀;y₀;z₀).

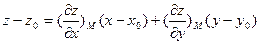(9¹)

і рівняння нормалі

(10¹)

Приклад: Знайти рівняння дотичної площини і нормалі до поверхні z=P+x²+y² в т .М(1;1;3).

Розв’язування.

Рівняння дотичної площини

z-3=2(x-1)+2(y-1);

z-3=2x-2+2y-2;

2x+2y-z=1.

Рівняння нормалі:

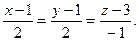
4. Означення. Функція z=f(x;y) має максимум (мінімум) в точці М(x₀;y₀), якщо в її околі (f(x;y)<f(x₀;y₀)).

Це означення поширюється і на функції більшої кількості змінних.

Максимуми і мінімуми функції називаються екстремумами, а точки в яких вони досягаються – точками екстремуму.

Зрозуміло, що якщо у функції f зафіксувати всі змінні, крім однієї, то отримаємо функцію однієї змінної, яка буде мати екстремум там же, що й функція кількох змінних. Звідси слідує, що в цій точці значення відповідної частинної похідної або дорівнює 0, або не існує.

Для знаходження екстремумів:

1. Знаходимо критичні точки, тобто ті в яких частинні похідні 1-го порядку рівні нулеві: (якщо всі частинні похідні = 0, то така точка є стаціонарною) або не існують.

2. Визначаємо величини:

.

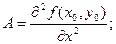
3. Складаємо дискримінант D=АС-В².

4. Якщо D>0, то функція має в М₀ – екстремум. А саме: якщо А>0 (чи С>0) – мінімум; якщо А<0 (чи C>0) – мінімум; якщо А<0 (чи C<0) – максимум.

Якщо D<0, то в точці М₀ екстремуму немає.

Якщо D=0, то проблема потребує додаткових досліджень.

Приклад. Знайти екстремум функції z=x²+xy+y²-3x-6y

Розв’язування.

1)

2) Знаходим стаціонарні точки: 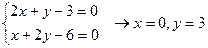М(0;3)

3)

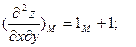
4) D=2^.2-1=3>0; A>0

в т. М₀(0;3) z=x²+xy+y²-3x-6y має мінімум.

Z_min=0²+0^.3+3^.0-6^.3=9-18=-9.

5. Означення. Умовним екстремумом функції z=f(x;y) називається екстремум цієї функції, досягнутий за умови, що х i y зв‘язані рівнянням зв’язку j(х,у)=0.

Його знаходження зведемо до дослідження на звичайний екстремум функції Лагранжа

,

де: l-невизначений множник.

Тоді:

Звідси знайдемо х, у, l.

Для знаходження найбільшого і найменшого значення в замкнутій області:

1) Знайти стаціонарні точки в цій області і обчислити значення функцій в цих точках;

2) Знайти найбільше і найменше значення на границі області;

3) З всіх значень вибрати найбільше і найменше.

Приклад: Знайти екстремуми z=xy, якщо х і у зв’язані рівнянням 2х+3у-5=0.

Розв’язування.

u=xy+l(2x+3y-5)

.

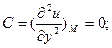
Дата добавления: 2017-02-01