
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.2 Дії над комплексними числами
|
|
|
|
Мета. Ввести поняття арифметичних дій над комплексними числами, використовуючи формулу Муавра, навчитися підносити комплексні числа до степеня та добувати корені з комплексних чисел.
План.
1. Арифметичні дії над комплексними числами.
2. Формула Муавра та її застосування.
1. Найпростіші арифметичні дії над комплексними числами виконуються за формулами:
 ;
;
 ;
;
 .
.
Ділення комплексних чисел зводиться до множення чисельника та знаменника виразу на число, спряжене до знаменника, в результаті чого знаменник перетворюється в дійсне число:
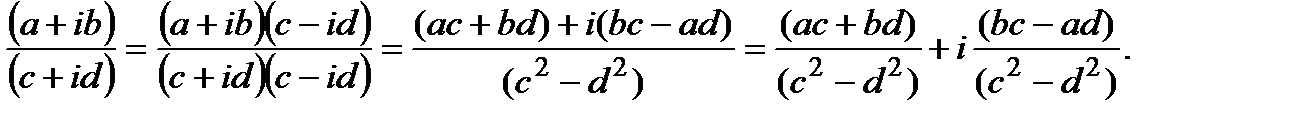
Зауважимо, що множення і ділення комплексних чисел, а також піднесення в натуральний степінь і добування кореня, як правило, зручно проводити, попередньо записавши комплексні числа в показниковій формі.
Нехай  i
i  , тоді
, тоді
 . (1)
. (1)
Тут ми скористались властивістю комплексного степеня числа е.
Звідси легко отримуємо
 . (2)
. (2)
Приклад 1. Знайти частку  .
.
Розв’язування. Помноживши чисельник та знаменник дробу на число, спряжений знаменнику, отримаємо
 .
.
З означення дії множення комплексних чисел випливає, що для кожного а ≠ 0 існує обернене комплексне число, тобто таке число b, що ab = 1,
Справді. Нехай а = r (  ), b = x(
), b = x(  ). Зрозуміло, що 1 =
). Зрозуміло, що 1 =  . Тепер маємо:
. Тепер маємо:
rx = 1,
φ + y = 0,
звідки x =  (r ≠ 0), оскільки a ≠ 0), y = - φ. Отже,
(r ≠ 0), оскільки a ≠ 0), y = - φ. Отже,
b = a-1 =  .
.
Цей результат дає можливість ввести дію ділення комплексних чисел. Під часткою  розумітимемо розв’язок рівняння ax = b.
розумітимемо розв’язок рівняння ax = b.
Безпосередня перевірка показує, що розв’язком рівняння буде число x = a-1 ∙ b. Таким чином, якщо a = r ( ), b =
), b =  , то
, то
 (3)
(3)
Отже, маємо таке правило ділення: модуль частки двох комплексних чисел дорівнює відношенню модулів діленого і дільника, а аргумент частки – різниці аргументів діленого і дільника.
2. Якщо a = r (  ) – комплексне число, а n – натуральне число, то, як звичайно покладаємо
) – комплексне число, а n – натуральне число, то, як звичайно покладаємо
| n - раз |
З правила множення випливає, що
 . (4)
. (4)
Формулу (4) називають формулою Муавра.
Оскільки  , то
, то  .
.
Це дає можливість множити комплексні числа, записані в нормальній формі. Справді, дії множення і додавання комплексних чисел пов’язані дистрибутивним законом. Звідси випливає, що числа  і
і 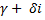 перемножаються за звичайним правилом розкриття дужок з урахуванням того, що
перемножаються за звичайним правилом розкриття дужок з урахуванням того, що  .
.
 . (5)
. (5)
Легко вивести і формулу ділення комплексних чисел у нормальній формі. Нехай  ,
, 
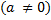 . Тоді
. Тоді

Цю формулу зручніше запам’ятати у скороченому вигляді.
Для цього введемо таке означення, корисне і в інших випадках. Комплексні числа 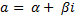 і
і 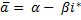 називатимемо спряженими. Очевидно,
називатимемо спряженими. Очевидно,  .
.
Зрозуміло, що точки площини, які відповідають спряженим комплексним числам, розміщені симетрично відносно осі ОX. Зокрема, якщо a – дійсне число (β = 0), то  . Якщо a =
. Якщо a =  , то, як легко побачити,
, то, як легко побачити,  . Спряжені комплексні числа мають однакові модулі і протилежні аргументи. Зокрема,
. Спряжені комплексні числа мають однакові модулі і протилежні аргументи. Зокрема,
 (6)
(6)
Добуток спряжених комплексних чисел дорівнює квадрату їх модуля.
Тепер формулу ділення комплексних чисел у нормальній формі можна записати так:
>  (7)
(7)
Коренем степення n (n  ) з комплексного числа a називається таке комплексне число z, що
) з комплексного числа a називається таке комплексне число z, що 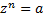 .
.
Очевидно, якщо а = 0, то 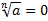 , тому далі вважатимемо, що
, тому далі вважатимемо, що 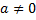 .
.
Нехай a =  – дане комплексне число, а z =
– дане комплексне число, а z =  – корінь степення n з a. Тоді
– корінь степення n з a. Тоді
 .
.
Рівність двох комплексних означає, що їх модулі однакові, а аргументи їх аргументи різняться на кут, кратний 2π. Отже,  . Звідси
. Звідси
 (8)
(8)

|

|

|
| r |
| Z1 |
| Z2 |
| Z3 |
 слід розуміти додатнє значення корення, оскільки
слід розуміти додатнє значення корення, оскільки  , і
, і| 0 |

|
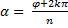 , k
, k  . (9)
. (9)
При k = k1 і k = k2 матимемо те саме значення 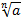 ,
,
 , де l – ціле число, тобто, коли
, де l – ціле число, тобто, коли
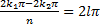 , або
, або  =
= 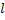 .
.
Отже, якщо  ділиться на
ділиться на 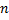 , то при k = k1 і k = k2 матимемо той самий корінь степеня
, то при k = k1 і k = k2 матимемо той самий корінь степеня 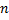 з a. Якщо
з a. Якщо  не ділиться на
не ділиться на 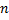 , то відповідні значення α не різнитимуться на кут, кратний 2π, і при k = k1 і k = k2 матимемо різні значення
, то відповідні значення α не різнитимуться на кут, кратний 2π, і при k = k1 і k = k2 матимемо різні значення 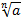 . Числа 0, 1, 2, …,
. Числа 0, 1, 2, …, 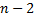 ,
,  мають ту властивість, що різниця між будь-якими двома з них не ділиться на
мають ту властивість, що різниця між будь-якими двома з них не ділиться на 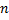 , бо вона за модулем менша, ніж
, бо вона за модулем менша, ніж 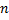 .
.
Отже, при k = 0, 1, 2, …, 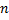 – 1 дістанемо
– 1 дістанемо 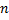 різних значень
різних значень 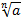 . Оскільки будь-яке ціле число k можна зап3сати у вигляді
. Оскільки будь-яке ціле число k можна зап3сати у вигляді
 ,
,
де  і
і  – цілі числа, причому 0 ≤
– цілі числа, причому 0 ≤  ≤
≤ 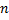 – 1, то інші значення
– 1, то інші значення  вже не можуть дати нових коренів.
вже не можуть дати нових коренів.
Отже, приходимо до такого висновку: 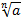 має
має 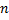 значень, модулі яких обчислюються за формулою (8) (вони всі рівні між собою), а аргументи подаються формулою (9), в якій треба по черзі покласти k = 0, 1, 2, …,
значень, модулі яких обчислюються за формулою (8) (вони всі рівні між собою), а аргументи подаються формулою (9), в якій треба по черзі покласти k = 0, 1, 2, …, 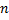 – 1.
– 1.
При двох послідовних значеннях k матимемо два значення α, що різняться між собою на  . Отже, корені лежать на колі радіуса
. Отже, корені лежать на колі радіуса  з центрому початку координат і ділять це коло на
з центрому початку координат і ділять це коло на 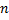 рівних частин.
рівних частин.
Приклад 2. Знайти 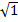 .
.
Розв’язування. 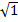 має два значення ±1.
має два значення ±1.
Приклад 2. Знайти 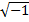 .
.
Розв’язування.
 .
.
 ,
,  .
.
Отже,  ,
, 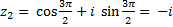 .
.
Приклад 3. Знайти всі значення  .
.
Розв’язування.
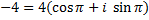 .
.
 ,
, 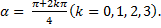
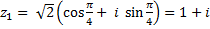 ,
,
 ,
,
 ,
,
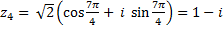 .
.
Корені  ,
,  ,
,  ,
,  ділять коло радіуса
ділять коло радіуса 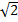 на 4 рівні частини. Це точки перетину кола з бісектрисами координатних кутів.
на 4 рівні частини. Це точки перетину кола з бісектрисами координатних кутів.
Приклад 4. Знайти всі значення 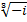 .
.
Розв’язування.
 .
.
 ,
, 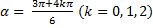 .
.
 ,
,
 ,
,
 .
.
Корені  ,
,  ,
,  ділять коло радіуса 1 на 3 рівні частини.
ділять коло радіуса 1 на 3 рівні частини.
Особливо цікаві корені степеня n з 1. З попередніх міркувань випливає, що вони ділять коло радіуса 1 з центром у початку координат на n рівних частин, причому, однією з точок поділу буде точка 1 на осі ОX, бо 1 буде одним із значень  (при
(при  ).
).
Якщо  корені степеня n з 1, то їх добуток і частка також будуть коренями степеня n з 1, як це випливає з рівностей
корені степеня n з 1, то їх добуток і частка також будуть коренями степеня n з 1, як це випливає з рівностей
 ,
,
 .
.
Одним із значень  буде
буде  .
.
Легко побачити, що числами  вичерпуються всі корені з 1. Число
вичерпуються всі корені з 1. Число 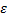 називається первинним коренем степеня n з 1.
називається первинним коренем степеня n з 1.
Якщо а – додатне число, то  , тому
, тому
 ,
,
Ця формула показує, що всі корені степеня n з додатного числа можна дістати, помноживши арифметичне значення кореня з цього числа на всі корені степеня n з 1. Більш загально, усі корені степеня n з будь-якого комплексного числа а можна дістати, помноживши яке-небудь одне значення 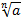 на всі корені степеня n з 1. Це випливає з рівності
на всі корені степеня n з 1. Це випливає з рівності
 .
.
Контрольні питання:
1. Як виконувати дії над комплесними числами, записаними в нормальній формі?
2. Як виконувати множення та ділення комплексних чисел, поданих в показниковій формі?
3. Яке число називається оберненим комплексним числом?
4. Запишіть формулу Муавра.
5. Що називається коренем степеня n з комплексного числа?
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 91; Нарушение авторских прав?; Мы поможем в написании вашей работы!